6387: 有向图的拓扑序列
[Creator : ]
Description
【知识点】
拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
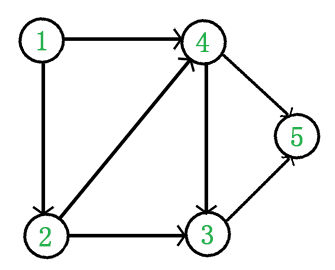
上图是一个 DAG 图,那么如何写出它的拓扑排序呢?这里说一种比较常用的方法:
1:从 DAG 图中选择一个 没有前驱(即入度为 $0$)的顶点并输出。
2:从图中删除该顶点和所有以它为起点的有向边。
3:重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
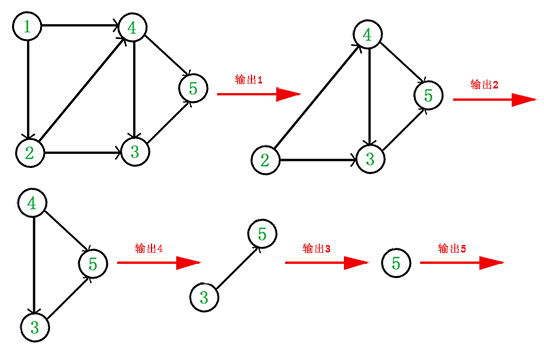
于是,得到拓扑排序后的结果是 $\{1, 2, 4, 3, 5 \}$。通常,一个有向无环图可以有一个或多个拓扑排序序列。
【问题】
给定一个 $n$ 个点 $m$ 条边的有向图,点的编号是 $1$ 到 $n$,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 $-1$。
若一个由图中所有点构成的序列 $A$ 满足:对于图中的每条边 $(x,y)$,$x$ 在 $A$ 中都出现在 $y$ 之前,则称 $A$ 是该图的一个拓扑序列。
拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。

上图是一个 DAG 图,那么如何写出它的拓扑排序呢?这里说一种比较常用的方法:
1:从 DAG 图中选择一个 没有前驱(即入度为 $0$)的顶点并输出。
2:从图中删除该顶点和所有以它为起点的有向边。
3:重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

于是,得到拓扑排序后的结果是 $\{1, 2, 4, 3, 5 \}$。通常,一个有向无环图可以有一个或多个拓扑排序序列。
【问题】
给定一个 $n$ 个点 $m$ 条边的有向图,点的编号是 $1$ 到 $n$,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 $-1$。
若一个由图中所有点构成的序列 $A$ 满足:对于图中的每条边 $(x,y)$,$x$ 在 $A$ 中都出现在 $y$ 之前,则称 $A$ 是该图的一个拓扑序列。
Input
第一行包含两个整数 $n$ 和 $m$。
接下来 $m$ 行,每行包含两个整数 $x$ 和 $y$,表示存在一条从点 $x$ 到点 $y$ 的有向边 $(x,y)$。
接下来 $m$ 行,每行包含两个整数 $x$ 和 $y$,表示存在一条从点 $x$ 到点 $y$ 的有向边 $(x,y)$。
Output
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 $-1$。
否则输出 $-1$。
Constraints
$1≤n,m≤2 \times 10^5$
Sample 1 Input
3 3
1 2
2 3
1 3
Sample 1 Output
1 2 3