6321: ABC232 —— C - Graph Isomorphism
[Creator : ]
Description
Takahashi and Aoki each have a toy made by attaching $M$ cords to $N$ balls.
In Takahashi's toy, the balls are numbered $1, \dots, N$, and the $i$-th cord ties Ball $A_i$ and $B_i$.
Similarly, in Aoki's toy, the balls are numbered $1, \dots, N$, and the $i$-th cord ties Ball $C_i$ and $D_i$.
In each toy, no cord ties a ball to itself, and no two balls are tied by two or more different cords.
Snuke is wondering whether the two toys have the same shape.
Here, they are said to have the same shape when there is a sequence $P$ that satisfies the conditions below.
In Takahashi's toy, the balls are numbered $1, \dots, N$, and the $i$-th cord ties Ball $A_i$ and $B_i$.
Similarly, in Aoki's toy, the balls are numbered $1, \dots, N$, and the $i$-th cord ties Ball $C_i$ and $D_i$.
In each toy, no cord ties a ball to itself, and no two balls are tied by two or more different cords.
Snuke is wondering whether the two toys have the same shape.
Here, they are said to have the same shape when there is a sequence $P$ that satisfies the conditions below.
- $P$ is a permutation of $(1, \dots, N)$.
-
For every pair of integers $i, j$ between $1$ and $N$ (inclusive), the following holds.
- Balls $i$ and $j$ in Takahashi's toy are tied by a cord if and only if Balls $P_i$ and $P_j$ in Aoki's toy are tied by a cord.
Input
Input is given from Standard Input in the following format:
$N\ M$
$A_1\ B_1$
$\vdots$
$A_M\ B_M$
$C_1\ D_1$
$\vdots$
$C_M\ D_M$
$N\ M$
$A_1\ B_1$
$\vdots$
$A_M\ B_M$
$C_1\ D_1$
$\vdots$
$C_M\ D_M$
Output
If the two toys have the same shape, print Yes; otherwise, print No.
Constraints
$1≤N≤8$
$0 \leq M \leq \frac{N(N - 1)}{2}$
$1 \leq A_i \lt B_i \leq N \, (1 \leq i \leq M)$
$(A_i, B_i) \neq (A_j, B_j) \, (i \neq j)$
$1 \leq C_i \lt D_i \leq N \, (1 \leq i \leq M)$
$(C_i, D_i) \neq (C_j, D_j) \, (i \neq j)$
All values in input are integers.
$0 \leq M \leq \frac{N(N - 1)}{2}$
$1 \leq A_i \lt B_i \leq N \, (1 \leq i \leq M)$
$(A_i, B_i) \neq (A_j, B_j) \, (i \neq j)$
$1 \leq C_i \lt D_i \leq N \, (1 \leq i \leq M)$
$(C_i, D_i) \neq (C_j, D_j) \, (i \neq j)$
All values in input are integers.
Sample 1 Input
4 4
1 2
1 3
1 4
3 4
1 3
1 4
2 3
3 4
Sample 1 Output
Yes
Takahashi's toy is illustrated on the left in the figure below, and Aoki's is illustrated on the right.
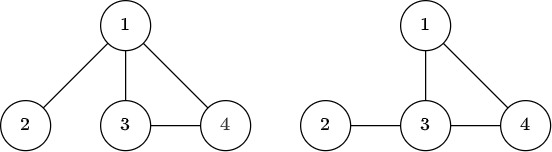
The following figure shows that the two toys have the same shape. The condition in the statement is satisfied when $P = (3, 2, 1, 4)$, for example.
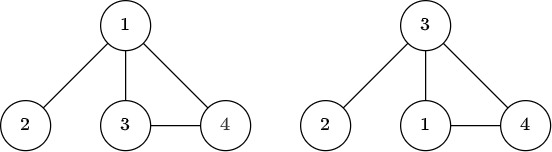

The following figure shows that the two toys have the same shape. The condition in the statement is satisfied when $P = (3, 2, 1, 4)$, for example.

Sample 2 Input
5 6
1 2
1 3
1 4
3 4
3 5
4 5
1 2
1 3
1 4
1 5
3 5
4 5
Sample 2 Output
No
The two toys do not have the same shape.
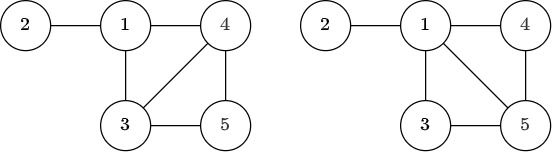

Sample 3 Input
8 0
Sample 3 Output
Yes