Takahashi won a claw machine competition and was awarded "all-you-can-stuff" gold blocks.
There are unlimited numbers of blocks weighing $w_1, w_2, \dots, w_K$ kilograms each, and an unlimited number of bags weighing $1$ kilogram each to stuff them.
Takahashi can bring home one non-empty bag.
A bag can contain zero or more other non-empty bags and zero or more gold blocks.
After arranging a truck with a load capacity of WW kilograms, he gets interested in the number of ways to stuff gold blocks and bring home a bag that weighs $w$ kilograms in total for $w = 2, 3, \dots, W$.
Find the number, modulo $998244353$, of possible states of the bag for each $w = 2, 3, \dots, W$. Here,

• two gold blocks are said to be the same when their weights are the same;
• two bags are said to be in the same state when the two multisets whose elements are the bags and gold blocks in the two bags are the same.

Input is given from Standard Input in the following format:
$W\ K$
$w_1\ w_2\ \dots\ w_K$

Print the answer in $W - 1$ lines.
The $i$-th line should contain the count for $w = i + 1$.

$2≤W≤2.5×10^5$
$1 \leq K \leq W$
$1 \leq w_i \leq W (1 \leq i \leq K)$
$i \neq j \to w_i \neq w_j (1 \leq i,j \leq K)$
All values in input are integers.

1
2
4

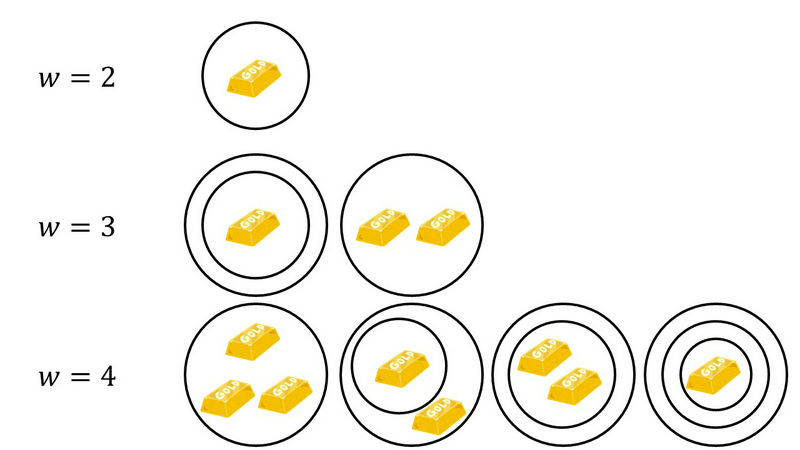
The figure below enumerates the possible states of the bag for $w = 2, 3, 4$. (A circle represents a bag.)