In a town divided into a grid with $N$ rows and $10^9$ columns, there are $N$ walls, numbered $1$ to $N$.
Wall ii ranges from the $L_i$-th column to the $R_i$-th column from the left in the $i$-th row from the top. (See also the figure at Sample Input and Output $1$.)
Takahashi has decided to destroy all $N$ walls.
With his superhuman strength, his one punch can damage consecutive $D$ columns at once.

• More formally, he can choose an integer $x$ between $1$ and $10^9 - D + 1$ (inclusive) to damage all walls that exist (or partly exist) in the $x$-th through $(x + D - 1)$-th columns and are not yet destroyed.

When a part of a wall is damaged, that whole wall will be destroyed by the impact of the punch.
(See also the figure at Sample Input and Output $1$.)
At least how many times does Takahashi need to punch to destroy all walls?

Input is given from Standard Input in the following format:
$N\ D$
$L_1\ R_1$
$L_2\ R_2$
$\vdots$
$L_N\ R_N$

Print the minimum number of punches needed to destroy all walls.

$1≤N≤2×10^5$
$1 \leq D \leq 10^9$
$1 \leq L_i \leq R_i \leq 10^9$
All values in input are integers.

2

The figure below describes the arrangements of walls in Sample Input $1$.



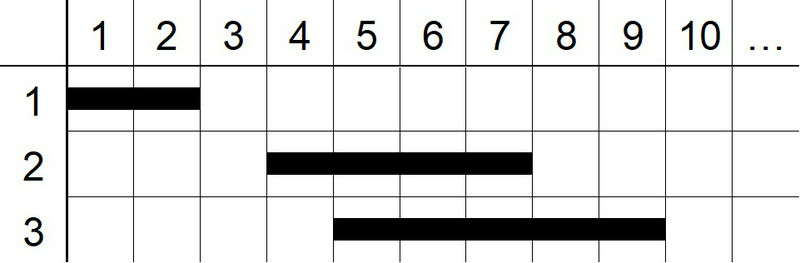
He can destroy all walls with two punches, such as the following. (Below, $\lbrack a, b \rbrack$ denotes the range from the $a$-th through $b$-th columns.)

• First, punch $\lbrack 2, 4 \rbrack$. The walls existing in $\lbrack 2, 4 \rbrack$ ― Walls $1$ and $2$ ― are damaged and destroyed.
• Second, punch $\lbrack 5, 7 \rbrack$. The wall existing in $\lbrack 5, 7 \rbrack$ ― Wall $3$ ― is damaged and destroyed.

It is also possible to destroy all walls with two punches in this way:

• First, punch $\lbrack 7, 9 \rbrack$ to destroy Walls $2$ and $3$.
• Second, punch $\lbrack 1, 3 \rbrack$ to destroy Wall $1$.

1

The difference from Sample Input/Output $1$ is that Wall $3$ now covers $\lbrack 4, 9 \rbrack$, not $\lbrack 5, 9 \rbrack$.
In this case, he can punch $\lbrack 2, 4 \rbrack$ to destroy all walls with one punch.