6254: 学习系列 —— 图论4:图的存储 3:邻接表
[Creator : ]
Description
【方法】
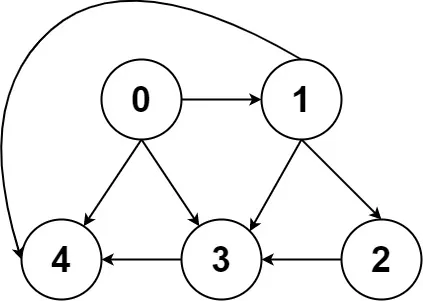
使用一个支持动态增加元素的数据结构构成的数组,如
上图对应的邻接表如下图所示。
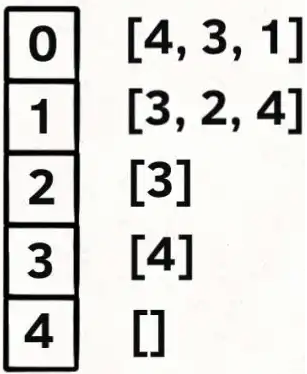
【参考代码】

使用一个支持动态增加元素的数据结构构成的数组,如
vector<int> adj[n + 1];来存边,其中 $\text{adj}$ 存储的是点 $u$ 的所有出边的相关信息(终点、边权等)。
上图对应的邻接表如下图所示。

【参考代码】
// C++ Version
#include <iostream>
#include <vector>
using namespace std;
int n, m;
vector<bool> vis;
vector<vector<int> > adj;
bool find_edge(int u, int v) {
for (int i = 0; i < adj.size(); ++i) {
if (adj[i] == v) {
return true;
}
}
return false;
}
void dfs(int u) {
if (vis) return;
vis = true;
for (int i = 0; i < adj.size(); ++i) dfs(adj[i]);
}
int main() {
cin >> n >> m;
vis.resize(n + 1, false);
adj.resize(n + 1);
for (int i = 1; i <= m; ++i) {
int u, v;
cin >> u >> v;
adj.push_back(v);
}
return 0;
}
# Python Version
vis = [False] * (n + 1)
adj = [[]] * (n + 1)
for i in range(1, m + 1):
u, v = map(lambda x:int(x), input().split())
adj.append(v)
def find_edge(u, v):
for i in range(0, len(adj)):
if adj[i] == v:
return True
return False
def dfs(u):
if vis:
return
vis = True
for i in range(0, len(adj)):
dfs(adj[i])
【复杂度】
查询是否存在 $u$ 到 $v$ 的边:(如果事先进行了排序就可以使用 二分查找 做到 )$O(log(d^+(u)))$。
遍历点 $u$ 的所有出边:$O(d^+(u))$。
遍历整张图:$O(n+m)$。
空间复杂度:$O(m)$。
【应用】
存各种图都很适合,除非有特殊需求(如需要快速查询一条边是否存在,且点数较少,可以使用邻接矩阵)。
尤其适用于需要对一个点的所有出边进行排序的场合。