学习系列 —— 图论3：图的存储 2：邻接矩阵 - Problem

【方法】

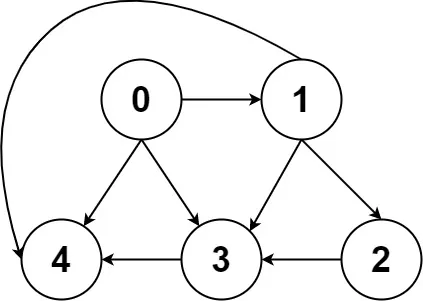
使用一个二维数组 adj 来存边，其中 adj[v] 为 $1$ 表示存在 $u$ 到 $v$ 的边，为 $0$ 表示不存在。如果是带边权的图，可以在 adj[v] 中存储 $u$ 到 $v$ 的边的边权。

【优点】
直观。
可以随机访问。
适合稠密图。
【缺点】
当图规模变大后，例如 $n > 2,000$，就可能导致 MLE。

【C++ 数组版】

//定义无穷大 
const LL INF=0x3f3f3f3f3f3f3f3f;

//定义邻接矩阵 
const int N=2e3+10;
LL g[N][N];

/*下面代码是针对有重边有自环*/
//初始化图，将所有边设置为无穷大 
memset(g, 0x3f, sizeof g);
//读取边 
for (LL i=1; i<=m; i++) {
	LL u,v,w;
	cin>>u>>v>>w;
	g[v]=min(g[v], w);
}

【使用 STL 的 Vector】

// C++ 使用 vector 版本
/*友情提醒：有些出题人会卡vector*/
#include <iostream>
#include <vector>

using namespace std;

int n, m;
vector<bool> vis;
vector<vector<bool> > adj;

bool find_edge(int u, int v) { return adj[v]; }

void dfs(int u) {
  if (vis) return;
  vis = true;
  for (int v = 1; v <= n; ++v) {
    if (adj[v]) {
      dfs(v);
    }
  }
}

int main() {
  cin >> n >> m;

  vis.resize(n + 1, false);
  adj.resize(n + 1, vector<bool>(n + 1, false));

  for (int i = 1; i <= m; ++i) {
    int u, v;
    cin >> u >> v;
    adj[v] = true;
  }

  return 0;
}

# Python Version
vis = [False] * (n + 1)
adj = [[False]] * (n + 1)

for i in range(1, m + 1):
    u, v = map(lambda x:int(x), input().split())
    adj[v] = True

def find_edge(u, v):
    return adj[v]

def dfs(u):
    if vis:
        return
    vis = True
    for v in range(1, n + 1):
        if adj[v]:
            dfs(v)

【复杂度】

查询是否存在某条边：$O(1)$。

遍历一个点的所有出边：$O(n)$。

遍历整张图：$O(n^2)$。

空间复杂度：$O(n^2)$。

【应用】

邻接矩阵只适用于没有重边（或重边可以忽略）的情况。

其最显著的优点是可以 $O(1)$ 查询一条边是否存在。

由于邻接矩阵在稀疏图上效率很低（尤其是在点数较多的图上，空间无法承受），所以一般只会在稠密图上使用邻接矩阵。

6253: 学习系列 —— 图论3：图的存储 2：邻接矩阵

Description

HINT

Source/Category