图 (Graph) 是一个二元组 $G=(V(G),E(G)$。其中 $V(G)$ 是非空集，称为 点集 (Vertex set)，对于 $V$ 中的每个元素，我们称其为 顶点 (Vertex) 或 节点 (Node)，简称 点； $E(G)$ 为 $V(G)$ 各结点之间边的集合，称为 边集 (Edge set)。

常用 $G=(V,E)$ 表示图。

当 $V,E$ 都是有限集合时，称 $G$ 为 有限图。

当 $V$ 或 $E$ 是无限集合时，称 $G$ 为 无限图。

图有多种，包括 无向图 (Undirected graph)，有向图 (Directed graph)，混合图 (Mixed graph) 等。

【无向图】

若 $G$ 为无向图，则 $E$ 中的每个元素为一个无序二元组 $(u,v)$，称作 无向边 (Undirected edge)，简称 边 (Edge)，其中 。设 $u,v \in V$，则 $u$ 和 $v$ 称为 $e$ 的 端点 (Endpoint)。如下图。

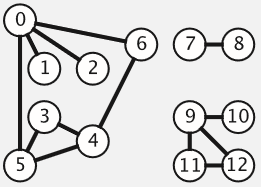
【有向图】

若 $G$ 为有向图，则 $E$ 中的每一个元素为一个有序二元组 $(u,v)$，有时也写作 $u \rightarrow v$，称作 有向边 (Directed edge) 或 弧 (Arc)，在不引起混淆的情况下也可以称作 边 (Edge)。设 $e=u \rightarrow v$，则此时 $u$ 称为 $e$ 的 起点 (Tail)，$v$ 称为 $e$ 的 终点 (Head)，起点和终点也称为 $e$ 的 端点 (Endpoint)。并称 $u$ 是 $v$ 的直接前驱，$v$ 是 $u$ 的直接后继。如下图。

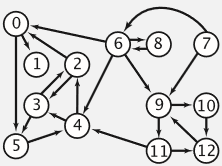
【混合图】

若 $G$ 为混合图，则 $E$ 中既有向边，又有无向边。

【加权图】

若 $G$ 的每条边 $e_k=(u_k, v_k)$ 都被赋予一个数作为该边的 权，则称 $G$ 为 赋权图。如果这些权都是正实数，就称 $G$ 为 正权图。

图 $G$ 的点数 $|V(G)|$ 也被称作图 $G$ 的 阶 (Order)。

形象地说，图是由若干点以及连接点与点的边构成的。

 
【相邻】

在无向图 $G=(V,E)$ 中，若点 $v$ 是边 $e$ 的一个端点，则称 $v$ 和 $e$ 是 关联的 (Incident) 或 相邻的 (Adjacent)。对于两顶点 $u$ 和 $v$，若存在边 $(u,v)$，则称 $u$ 和 $v$ 是 相邻的 (Adjacent)。

一个顶点 $v \in V$ 的 邻域 (Neighborhood) 是所有与之相邻的顶点所构成的集合，记作 $N(v)$。

一个点集 $S$ 的邻域是所有与 $S$ 中至少一个点相邻的点所构成的集合，记作 $N(S)$，即：$N(S)=\bigcup_{v \in S} N(v)$

【度数】

与一个顶点 $v$ 关联的边的条数称作该顶点的 度 (Degree)，记作 $d(v)$。特别地，对于边 $(u,v)$，则每条这样的边要对 $d(v)$ 产生 $2$ 的贡献。

对于无向简单图，有 $d(v)=|N(v)|$。

握手定理（又称图论基本定理）：对于任何无向图 $G=(V,E)$，有 $\sum_{v \in V} d(v)=2 \left| E \right|$。

推论：在任意图中，度数为奇数的点必然有偶数个。

若 $d(v)=0$，则称 $v$ 为 孤立点 (Isolated vertex)。

若 $d(v)=1$，则称 $v$ 为 叶节点 (Leaf vertex)/悬挂点 (Pendant vertex)。

若 $2 \mid d(v)$，则称 $v$ 为 偶点 (Even vertex)。

若 $2 \nmid d(v)$，则称 $v$ 为 奇点 (Odd vertex)。图中奇点的个数是偶数。

若 $d(v)=|V|-1$，则称 $v$ 为 支配点 (Universal vertex)。

对一张图，所有节点的度数的最小值称为 $G$ 的 最小度 (Minimum degree)，记作 $\delta(G)$；最大值称为 最大度 (Maximum degree)，记作 $\Delta(G)$。即：$\delta(G)=\min_{v \in G} d(v),\ \Delta(G)=\max_{v in G} d(v)$。

在有向图 $G=(V,E)$ 中，以一个顶点 $v$ 为起点的边的条数称为该顶点的 出度 (Out-degree)，记作 $d^+(v)$。以一个顶点 $v$ 为终点的边的条数称为该节点的 入度 (In-degree)，记作 $d^-(v)$。显然 $d^+(v)+d^-(v)=d(v)$。

对于任何有向图 $G=(V,E)$，有：$\sum_{v \in V}d^+(v)=\sum_{v \in V}d^-(v)=|E|$

若对一张无向图 $G=(V,E)$，每个顶点的度数都是一个固定的常数 $k$，则称 $G$ 为 $k$- 正则图 ($k$-Regular Graph)。

如果给定一个序列 a，可以找到一个图 G，以其为度数列，则称 a 是 可图化 的。

如果给定一个序列 a，可以找到一个简单图 G，以其为度数列，则称 a 是 可简单图化 的。

【简单图】

自环 (Loop)：对 $E$ 中的边 $e=(u,v)$，若 $u=v$，则 $e$ 被称作一个自环。

重边 (Multiple edge)：若 $E$ 中存在两个完全相同的元素（边）$e_1,e_2$，则它们被称作（一组）重边。

简单图 (Simple graph)：若一个图中没有自环和重边，它被称为简单图。具有至少两个顶点的简单无向图中一定存在度相同的结点。（鸽巢原理）

如果一张图中有自环或重边，则称它为 多重图 (Multigraph)。
注意：

1、在无向图中 $(u,v)$ 和 $(v,u)$ 算一组重边，而在有向图中，$u \rightarrow v$ 和 $v \rightarrow u$ 不为重边。

2、在题目中，如果没有特殊说明，是可以存在自环和重边的，在做题时需特殊考虑。

【路径】

途径 (Walk)：途径是一个将若干个点连接起来的边的集合。形式化地说，途径 $w$ 是一个边的集合 $\{e_1,e_2,\ldots,e_k\}$，这个边集需要满足条件：存在一个由点构成的序列 $\{v_0,v_1,\ldots,v_k\}$ 满足 $e_i$ 的两个端点分别为 $v_{i-1}$ 和 $v_i$。这样的路径可以简写为 $v_0 \rightarrow v_1 \rightarrow v_2 \rightarrow \ldots \rightarrow v_k$。通常来说，边的数量 $k$ 被称作这条途径的 长度（如果边是带权的，长度通常指路径上的边权之和，题目中也可能另有定义）。

迹 (Trail)：对于一条途径 $w$，若 $\{e_1,e_2,\ldots,e_k\}$ 两两互不相同，则称 $w$ 是一条迹。

路径 (Path)（又称 简单路径 (Simple path))：对于一条迹 $w$，若其连接的点的序列中点两两不同，则称 $w$ 是一条路径。

回路 (Circuit)：对于一个迹 $w$，若 $v_0=v_k$，则称 $w$ 是一个回路。

环/圈 (Cycle)（又称 简单回路/简单环 (Simple circuit))：对于一个回路 $w$，若 $v_0=v_k$ 是点序列中唯一重复出现的点对，则称 $w$ 是一个环。