Problem6139--CSP-S2021 T2：括号序列（bracket）

6139: CSP-S2021 T2：括号序列（bracket）

[Creator : ]
Time Limit : 1.000 sec  Memory Limit : 256 MiB

SubmitSolved: 1Submit Num: 1StatisticsShowOff!

Description

小 w 在赛场上遇到了这样一个题：一个长度为 $n$ 且符合规范的括号序列，其有些位置已经确定了，有些位置尚未确定，求这样的括号序列一共有多少个。
身经百战的小 w 当然一眼就秒了这题，不仅如此，他还觉得一场正式比赛出这么简单的模板题也太小儿科了，于是他把这题进行了加强之后顺手扔给了小 c。
具体而言，小 w 定义“超级括号序列”是由字符 (、)、* 组成的字符串，并且对于某个给定的常数 $k$，给出了“符合规范的超级括号序列”的定义如下：
  1. ()、(S) 均是符合规范的超级括号序列，其中 S 表示任意一个仅由不超过 $k$ 个字符 * 组成的非空字符串（以下两条规则中的 S 均为此含义）；
  2. 如果字符串 A 和 B 均为符合规范的超级括号序列，那么字符串 AB、ASB 均为符合规范的超级括号序列，其中 AB 表示把字符串 A 和字符串 B 拼接在一起形成的字符串；
  3. 如果字符串 A 为符合规范的超级括号序列，那么字符串 (A)、(SA)、(AS) 均为符合规范的超级括号序列。
  4. 所有符合规范的超级括号序列均可通过上述 3 条规则得到。
例如，若 $k = 3$，则字符串 ((**()*(*))*)(***) 是符合规范的超级括号序列，但字符串 *()、(*()*)、((**))*)、(****(*)) 均不是。特别地，空字符串也不被视为符合规范的超级括号序列。
现在给出一个长度为 $n$ 的超级括号序列，其中有一些位置的字符已经确定，另外一些位置的字符尚未确定（用 ? 表示）。小 w 希望能计算出：有多少种将所有尚未确定的字符一一确定的方法，使得得到的字符串是一个符合规范的超级括号序列？
可怜的小 c 并不会做这道题，于是只好请求你来帮忙。

Input

第一行，两个正整数 $n,\ k$。
第二行，一个长度为 $n$ 且仅由 (、)、*、? 构成的字符串 S。

Output

输出一个非负整数表示答案对 ${10}^9 + 7$ 取模的结果。

Constraints


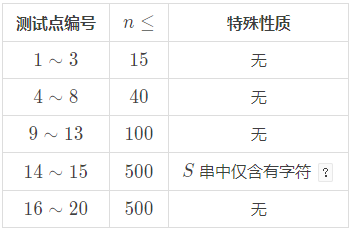
对于 $100\%$ 的数据，$1≤k≤n≤500$。

Sample 1 Input 

7 3
(*??*??

Sample 1 Output 

5

如下几种方案是符合规范的： 

(**)*()
(**(*))
(*(**))
(*)**()
(*)(**)

Sample 2 Input 

10 2
???(*??(?)

Sample 2 Output 

19

Sample 3 Input 

100 18
?*?????)?????*????????*??(*???????*????????????*???*?????*?????*??????*****??*??????????*???????????

Sample 3 Output 

860221334

HINT

相同题目：洛谷P7914。

Source/Category

 
Submit