5960: 学习系列——二维差分
[Creator : ]
Description
【知识点】
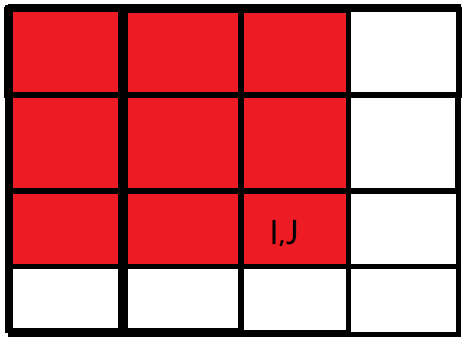
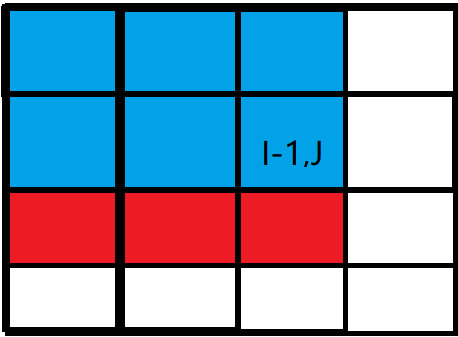
二维差分矩阵的计算类似于二维前缀和。下面我们用图来说明,假设我们需要计算第 $i$ 行第 $j$ 列的二维差分。
 tle="" align="" />
tle="" align="" />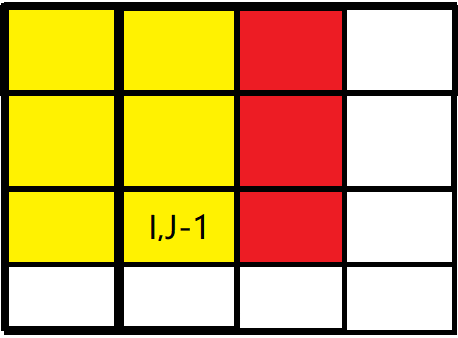 tle="" align="" />
tle="" align="" />
 tle="" align="" />
tle="" align="" />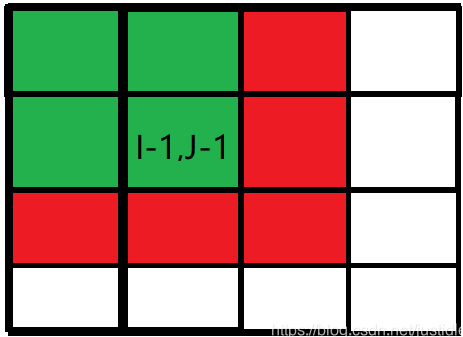 tle="" align="" />
tle="" align="" />
如上图所示,我们可以写出 $b_{i,\ j}=a_{i,\ j}-a_{i,\ j-1}-a_{i-1,\ j}+a_{i-1,\ j-1}$。
【要求】
给定一个 $n \times m$ 的二维数组 A,求出差分数组 B。
二维差分矩阵的计算类似于二维前缀和。下面我们用图来说明,假设我们需要计算第 $i$ 行第 $j$ 列的二维差分。
 tle="" align="" />
tle="" align="" /> tle="" align="" />
tle="" align="" />  tle="" align="" />
tle="" align="" /> tle="" align="" />
tle="" align="" /> 如上图所示,我们可以写出 $b_{i,\ j}=a_{i,\ j}-a_{i,\ j-1}-a_{i-1,\ j}+a_{i-1,\ j-1}$。
【要求】
给定一个 $n \times m$ 的二维数组 A,求出差分数组 B。
Input
第一行 $2$ 个正整数:$N,\ M\ (1 \leq N,\ M \leq 1,000)$。表示数组 A 为 $N$ 行 $M$ 列。
其后 $N$ 行,每行 $M$ 个整数 $A_{i,\ j}\ (1 \leq A_{i,\ j} \leq 10,000$)。
其后 $N$ 行,每行 $M$ 个整数 $A_{i,\ j}\ (1 \leq A_{i,\ j} \leq 10,000$)。
Output
对应二维数组的差分数组。
Sample 1 Input
3 4
1 2 4 3
5 1 2 4
6 3 5 9
Sample 1 Output
1 1 2 -1
4 -5 -1 3
1 1 1 2