5951: 判断一个点是否在三角形内
[Creator : ]
Description
给定三角形 $\triangle ABC$ 三个点坐标,以及一个点 $P$ 的坐标。请判断定 $P$ 是否在三角形 $\triangle ABC$ 内。
详细的部分可以参考,https://blackpawn.com/texts/pointinpoly/default.html。
【方法一:面积法】
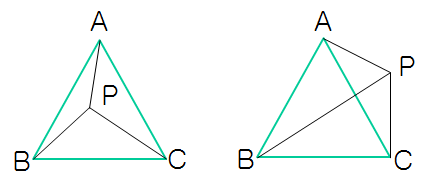
如上图所示,如果点 $P$ 在三角形 $\triangle ABC$ 内部,则 $S_{\triangle ABC} \equiv S_{\triangle PBC}+S_{\triangle PAB}+S_{\triangle PAC}$。
这样,我们根据海伦公式或者向量的叉乘。
【方法二:内角和法】
如上图所示。如果点 $P$ 在三角形 $\triangle ABC$ 内部,则 $\angle{PAC}+\angle{PAB}+\angle{PBA}+\angle{PBC}+\angle{PCB}+\angle{PCA} \equiv 180^\circ$。
但是这个方法效率相对较低,一般不使用。
【方法三:同向法】
点 $P$ 位于三角形内,会有这样一个规律,当我们沿着 $A \to B \to C \to A$ 的方向在三条边上行走时,你会发现点 $P$ 始终位于边 $AB$,$BC$ 和 $CA$ 的右侧。
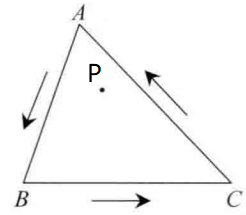
一般,我们使用该方法。
【方法四:重心法】
三角形的三个点在同一个平面上,如果选中其中一个点,其他两个点不过是相对该点的位移而已,比如选择点A作为起点,那么点B相当于在AB方向移动一段距离得到,而点C相当于在AC方向移动一段距离得到。
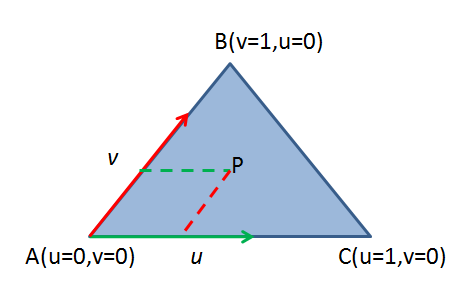
详细的部分可以参考,https://blackpawn.com/texts/pointinpoly/default.html。
【方法一:面积法】

如上图所示,如果点 $P$ 在三角形 $\triangle ABC$ 内部,则 $S_{\triangle ABC} \equiv S_{\triangle PBC}+S_{\triangle PAB}+S_{\triangle PAC}$。
这样,我们根据海伦公式或者向量的叉乘。
【方法二:内角和法】
如上图所示。如果点 $P$ 在三角形 $\triangle ABC$ 内部,则 $\angle{PAC}+\angle{PAB}+\angle{PBA}+\angle{PBC}+\angle{PCB}+\angle{PCA} \equiv 180^\circ$。
但是这个方法效率相对较低,一般不使用。
【方法三:同向法】
点 $P$ 位于三角形内,会有这样一个规律,当我们沿着 $A \to B \to C \to A$ 的方向在三条边上行走时,你会发现点 $P$ 始终位于边 $AB$,$BC$ 和 $CA$ 的右侧。

一般,我们使用该方法。
【方法四:重心法】
三角形的三个点在同一个平面上,如果选中其中一个点,其他两个点不过是相对该点的位移而已,比如选择点A作为起点,那么点B相当于在AB方向移动一段距离得到,而点C相当于在AC方向移动一段距离得到。

Input
一共包括两行。
第一行为 $6$ 个浮点数。分别表示 $(x_a,y_a),\ (x_b, y_b),\ (x_c,y_c)$,即 $\triangle ABC$ 三个顶点的坐标。
第二行为 $2$ 个浮点数,表示 $(x_p, y_p)$,即点 $P$ 的坐标。
第一行为 $6$ 个浮点数。分别表示 $(x_a,y_a),\ (x_b, y_b),\ (x_c,y_c)$,即 $\triangle ABC$ 三个顶点的坐标。
第二行为 $2$ 个浮点数,表示 $(x_p, y_p)$,即点 $P$ 的坐标。
Output
如果点在三角形内,输出 Yes。否则输出 No。
Sample 1 Input
1 1 3 1 2 3
2 2
Sample 1 Output
Yes
Sample 2 Input
1 1 3 1 2 3
0 0
Sample 2 Output
No