5947: 判断矩形是否相交
[Creator : ]
Description
在平面上,给出两个矩形,判断这两个矩形是否相交。
我们使用两个点来描述一个矩形,也就是所谓的左上角和右下角两个点。
判断矩形是否相交,我们是判断矩形不想交的情况。矩形不相交有下面所示的四种可能性。图片中蓝色代表矩形 1,红色代表矩形 2。
假设我们使用如下定义来表达一个点。
同样,我们可以使用左上角和右下角两个点来描述一个矩形 2,POINT L2, R2;
【情况一】

如上图所示。矩形 1 在矩形 2 的左边。那么这两个矩形的关系应该满足 L2.x>R1.x。
【情况二】

如上图所示。矩形 1 在矩形 2 的下边。那么这两个矩形的关系应该满足 R1.y>L2.y。
【情况三】
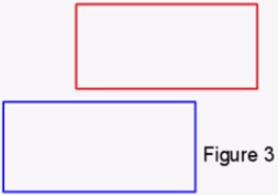
如上图所示。矩形 2 在矩形 1 的上边。那么这两个矩形的关系应该满足 R2.y>L1.y。
【情况四】

如上图所示。矩形 2 在矩形 1 的左边。那么这两个矩形的关系应该满足 L1.x>R2.x。
请注意,不同的题目提供的矩形坐标点描述可能不一样。
我们使用两个点来描述一个矩形,也就是所谓的左上角和右下角两个点。
判断矩形是否相交,我们是判断矩形不想交的情况。矩形不相交有下面所示的四种可能性。图片中蓝色代表矩形 1,红色代表矩形 2。
假设我们使用如下定义来表达一个点。
struct POINT {
double x,y;
};
这样,我们可以使用左上角和右下角两个点来描述一个矩形 1,POINT L1, R1; 同样,我们可以使用左上角和右下角两个点来描述一个矩形 2,POINT L2, R2;
【情况一】

如上图所示。矩形 1 在矩形 2 的左边。那么这两个矩形的关系应该满足 L2.x>R1.x。
【情况二】

如上图所示。矩形 1 在矩形 2 的下边。那么这两个矩形的关系应该满足 R1.y>L2.y。
【情况三】

如上图所示。矩形 2 在矩形 1 的上边。那么这两个矩形的关系应该满足 R2.y>L1.y。
【情况四】

如上图所示。矩形 2 在矩形 1 的左边。那么这两个矩形的关系应该满足 L1.x>R2.x。
请注意,不同的题目提供的矩形坐标点描述可能不一样。
Input
一共两行。
第一行包括 $4$ 个整数,$x_1,\ y_1,\ x_2,\ y_2$。$(x_1,\ y_1)$ 表示矩形的左上角,$(x_2,\ y_2)$ 表示矩形的右下角。
第二行包括 $4$ 个整数,$x_3,\ y_3,\ x_4,\ y_4$。$(x_3,\ y_3)$ 表示矩形的左上角,$(x_4,\ y_4)$ 表示矩形的右下角。
保证输入数据的合法性,坐标的绝对值不会超过 $10^{18}$。
第一行包括 $4$ 个整数,$x_1,\ y_1,\ x_2,\ y_2$。$(x_1,\ y_1)$ 表示矩形的左上角,$(x_2,\ y_2)$ 表示矩形的右下角。
第二行包括 $4$ 个整数,$x_3,\ y_3,\ x_4,\ y_4$。$(x_3,\ y_3)$ 表示矩形的左上角,$(x_4,\ y_4)$ 表示矩形的右下角。
保证输入数据的合法性,坐标的绝对值不会超过 $10^{18}$。
Output
如果这两个矩形相交,输出 Yes。否则输出 No。
Sample 1 Input
1 1 4 4
4 4 6 6
Sample 1 Output
Yes
Sample 2 Input
1 1 3 3
4 4 5 5
Sample 2 Output
No