【狄克斯特拉（Dijkstra）算法】
狄克斯特拉（Dijkstra）算法也是求解最短路径问题的算法，使用它可以求得从起点到终点的路径中权重总和最小的那条路径路径。狄克斯特拉算法的名称取自该算法的提出者埃德斯加· 狄克斯特拉，他在1972 年获得了图灵奖。
将图的顶点数设为 $n$、边数设为 $m$，那么如果事先不进行任何处理，该算法的时间复杂度就是 $O(n^2)$。不过，如果对数据结构进行优化，那么时间复杂度就会变为 $O(m+ nlogn)$。

这里我们设 $A$ 为起点、$G$ 为终点，来讲解狄克斯特拉算法。

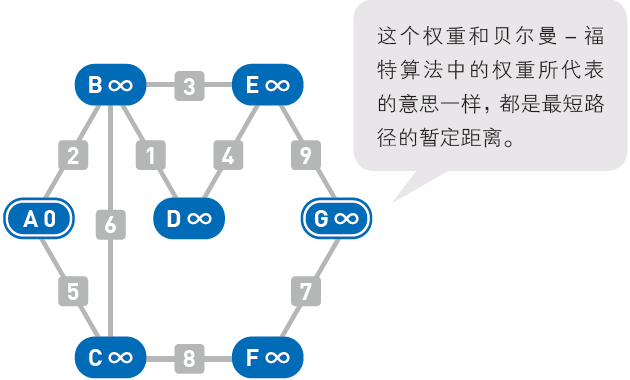
首先设置各个顶点的初始权重：起点为 $0$，其他顶点为无穷大（$+\infty$）。

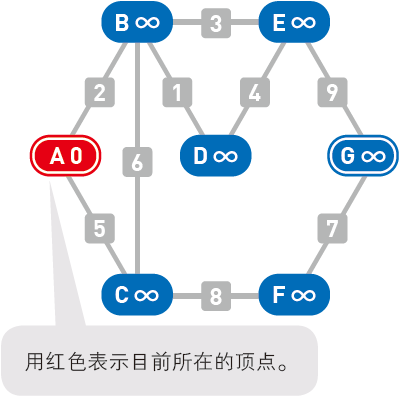
从起点出发。

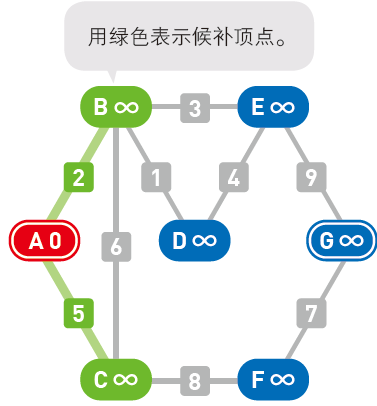
寻找可以从目前所在的顶点直达且尚未被搜索过的顶点，此处为顶点 $B$ 和顶点 $C$，将它们设为下一步的候补顶点。

计算各个候补顶点的权重。计算方法是“目前所在顶点的权重＋目前所在顶点到候补顶点的权重”。比如起点 $A$ 的权重是 $0$，那么顶点 $B$ 的权重就是 $0+2=2$。用同样的方法计算顶点 $C$，结果就是 $0+5=5$。

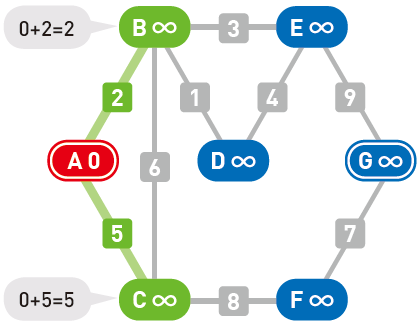
如果计算结果小于候补顶点的值，就更新这个值。顶点 $B$ 和顶点 $C$ 现在的权重都是无穷大，大于计算结果，所以更新这两个顶点的值。

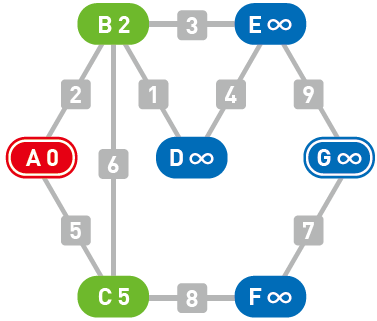
从候补顶点中选出权重最小的顶点。此处 $B$ 的权重最小，那么路径 $A \to B$ 就是从起点 $A$ 到顶点 $B$ 的最短路径。因为如果要走别的路径，那么必定会经过顶点 $C$，其权重也就必定会高于 $A \to B$ 这条路径。

确定了最短路径，移动到顶点 $B$。

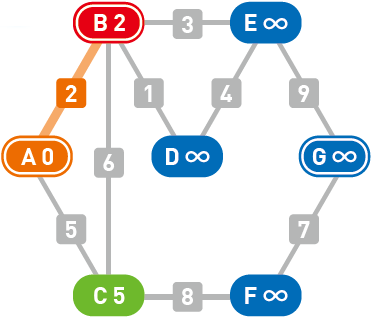
将可以从顶点 $B$ 直达的顶点设为新的候补顶点，于是顶点 $D$ 和顶点 $E$ 也成为了候补。目前有三个候补顶点 $C,D,E$。

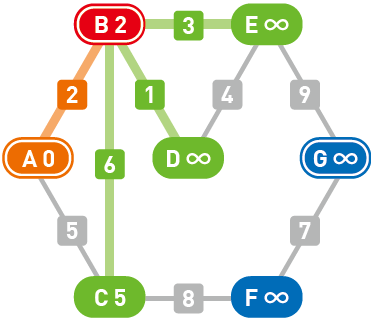
用相同的方法计算各个候补顶点的权重。从 $B$ 到 $C$ 的权重为 $2+6=8$，比 $C$ 当前的权重 $5$ 大，因此不更新这个值。

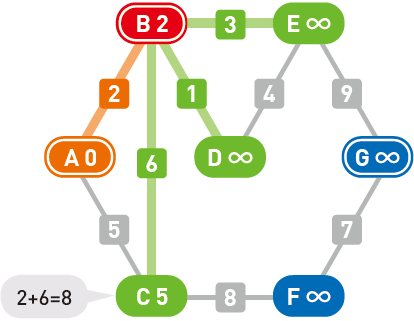
更新了剩下的顶点 $D$ 和 $E$。

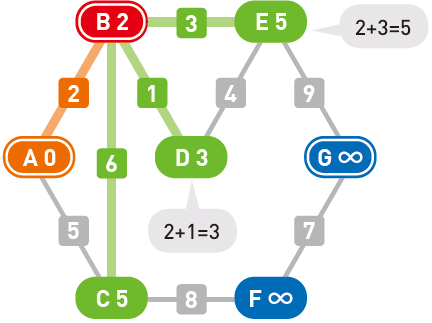
从候补顶点中选出权重最小的顶点。此处 $D$ 的权重最小，那么路径 $A \to B \to D$ 就是从起点 $A$ 到顶点 $D$ 的最短路径。

$A \to B \to D$ 这条路径是通过逐步从候补顶点中选择权重最小的顶点来得到的，所以如果经过其他顶点到达 $D$，其权重必定会大于这条路径。

要重复执行同样的操作直到到达终点 $G$ 为止。移动到顶点 $D$ 后算出了 $E$ 的权重，然而并不需要更新它（因为 $3+4=7$）。现在，两个候补顶点 $C$ 和 $E$ 的权重都为 $5$，所以选择哪一个都可以。

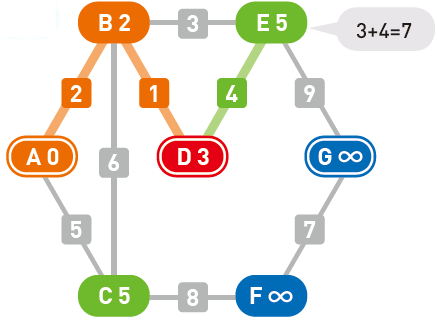
此处我们选择了 $C$，于是起点 $A$ 到顶点 $C$ 的最短路径便确定了。

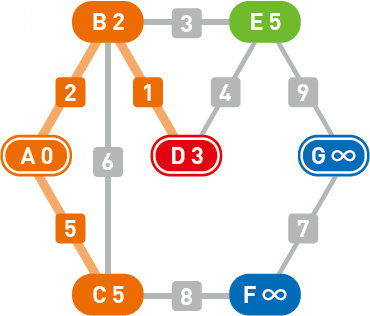
移动到 $C$ 后，顶点 $F$ 成为了新的候补顶点，且F的权重被更新为 $13$。此时的候补顶点中，$E$ 为 $5$、$F$ 为 $13$，所以……

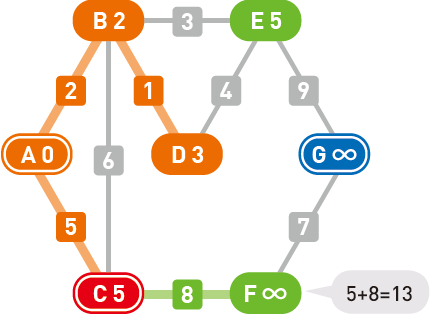
我们选择了权重更小的 $E$，起点 $A$ 到顶点 $E$ 的最短路径也就确定了下来。

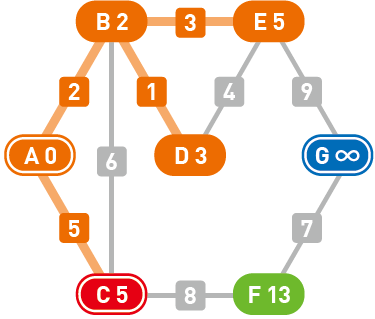
移动到 $E$。$G$ 成了新的候补顶点，其权重也被更新为 $14$。此时的候补顶点中，$F$ 为 $13$、$G$ 为 $14$，所以选择了 $F$。由此，起点 $A$ 到顶点 $F$ 的最短路径也就确定了下来。

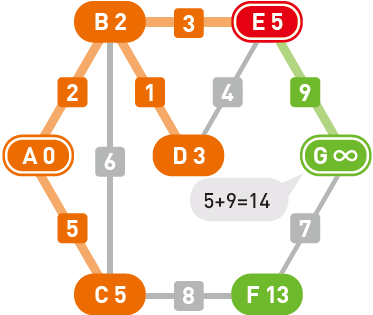
移动到 $F$。顶点 $G$ 的权重计算结果为 $13+7=20$，比现在的值 $14$ 要大，因此不更新它。由于候补顶点只剩 $G$ 了，所以选择 $G$，并确定了起点 $A$ 到顶点 $G$ 的最短路径。

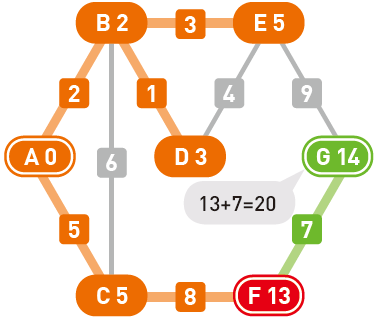
到达终点 $G$，搜索结束。

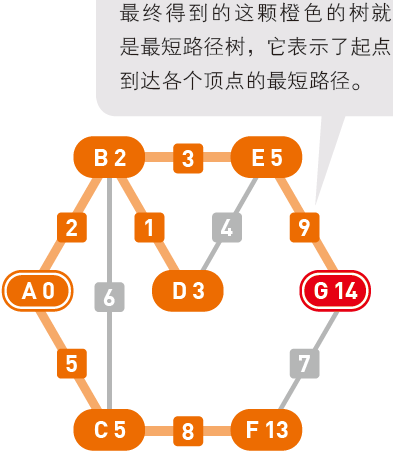
用粗线条标注的就是从起点 $A$ 到终点 $G$ 的最短路径。



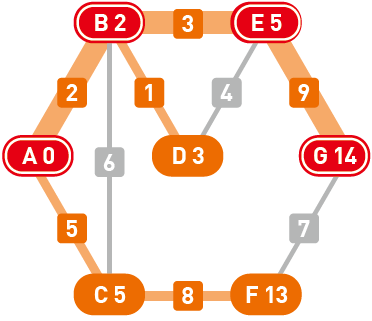
【问题描述】
给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

第一行包含三个整数 $n,m,s$，分别表示点的个数、有向边的个数、出发点的编号。
接下来 $m$ 行每行包含三个整数 $u,v,w$，表示一条 $u \to v$ 长度为 $w$ 的边。

输出一行 $n$ 个整数，第 $i$ 个表示 $s$ 到第 $i$ 个点的最短路径，若不能到达则输出 $-1$。

对于 $20\%$ 的数据：$1\le n \le 5,1\le m \le 15$；
对于 $40\%$ 的数据：$1\le n \le 100,1\le m \le 10^4$；
对于 $70\%$ 的数据：$1\le n \le 1000,1\le m \le 10^5$；
对于 $100\%$ 的数据：$1 \le n \le 10^4,1\le m \le 5\times 10^5,1\le u,v\le n,w\ge 0,\sum w< 2^{31}$，保证数据随机。