5800: 学习系列 —— 二分 —— 二分查找
[Creator : ]
Description
二分查找也是一种在有序数组中查找数据的算法。它只能查找已经排好序的数据。
二分查找通过比较数组中间的数据与目标数据的大小,可以得知目标数据是在数组的左边还是右边。因此,比较一次就可以把查找范围缩小一半。重复执行该操作就可以找到目标数据,或得出目标数据不存在的结论。
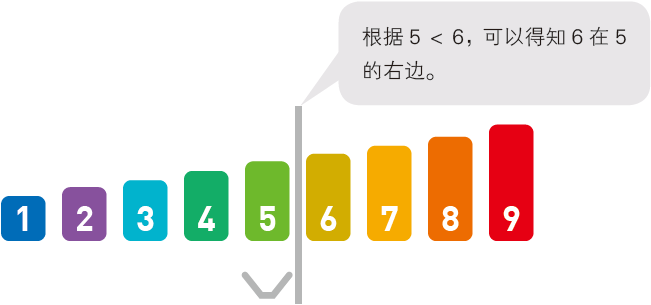
首先找到数组中间的数字,此处为 $5$。因为 $(1+9)/2=5$,使用下标进行加法。

将 $5$ 和要查找的数字 $6$ 进行比较。
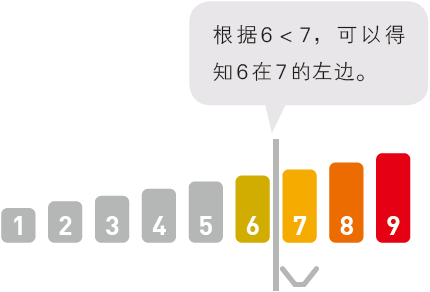
在剩下的数组中找到中间的数字,此处为 $7$。因为 $(6+9)/2=7$。

比较 $7$ 和 $6$。
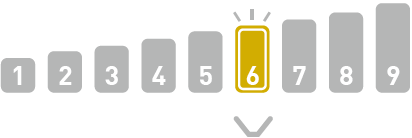
在剩下的数组中找到中间的数字,此处为 $6$。6=6,成功找到目标数字。
数据量为 $n$ 的数组,将其长度减半 $log_2n$ 次后,其中便只剩一个数据了。也就是说,在二分查找中重复执行“将目标数据和数组中间的数据进行比较后将查找范围减半”的操作 $log_2n$ 次后,就能找到目标数据(若没找到则可以得出数据不存在的结论),因此它的时间复杂度为 $O(logn)$。
特别注意:该方法只能查找唯一的数据。
二分查找通过比较数组中间的数据与目标数据的大小,可以得知目标数据是在数组的左边还是右边。因此,比较一次就可以把查找范围缩小一半。重复执行该操作就可以找到目标数据,或得出目标数据不存在的结论。
【查找过程】
下面我们在下边有序的数组,试试查找数字 $6$ 吧。该数组对应的下标索引为 $1,2,\cdots,9$。
首先找到数组中间的数字,此处为 $5$。因为 $(1+9)/2=5$,使用下标进行加法。

将 $5$ 和要查找的数字 $6$ 进行比较。

在剩下的数组中找到中间的数字,此处为 $7$。因为 $(6+9)/2=7$。

比较 $7$ 和 $6$。

在剩下的数组中找到中间的数字,此处为 $6$。6=6,成功找到目标数字。

数据量为 $n$ 的数组,将其长度减半 $log_2n$ 次后,其中便只剩一个数据了。也就是说,在二分查找中重复执行“将目标数据和数组中间的数据进行比较后将查找范围减半”的操作 $log_2n$ 次后,就能找到目标数据(若没找到则可以得出数据不存在的结论),因此它的时间复杂度为 $O(logn)$。
特别注意:该方法只能查找唯一的数据。
Input
模板代码
const int N=2e6+10;
LL a[N];
//在 [l,r] 中找到 x 的下标
LL bsearch(LL l, LL r, LL x) {
while (l<r) {
LL m=(l+r)/2;
if (a[m]==x) {
return m;
} else if (a[m]>x) {
r=m-1;
} else {
l=m+1;
}
}
return l;
}
Output
特别注意:
二分查找总是能找到一个需要的索引位置。我们需要对数据的合法性进行判断。
二分查找总是能找到一个需要的索引位置。我们需要对数据的合法性进行判断。