快速排序算法首先会在序列中随机选择一个基准值（pivot），然后将除了基准值以外的数分为“比基准值小的数”和“比基准值大的数”这两个类别，再将其排列成以下形式。
[ 比基准值小的数] 基准值 [ 比基准值大的数]
接着，对两个“[ ]”中的数据进行排序之后，整体的排序便完成了。对“[ ]”里面的数据进行排序时同样也会使用快速排序。
【过程】
在序列中随机选择一个基准值。这里选择了4。

将其他数字和基准值进行比较。小于基准值的往左移，大于基准值的往右移。

首先，比较3 和基准值4。

因为3 ＜ 4，所以将3 往左移。

接下来，比较5 和基准值4。

因为5 ＞ 4，所以将5 往右移。

对其他数字也进行同样的操作，最终结果如下图所示。

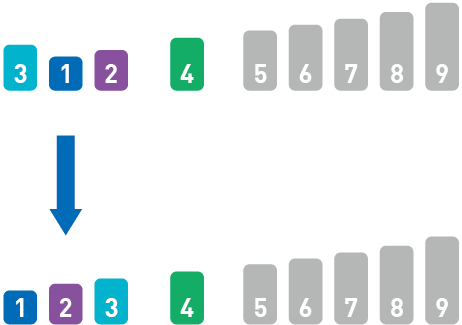
把基准值4 插入序列。这样，4 左边就是比它小的数字，右边就是比它大的数字。

分别对左边和右边的数据进行排序后，就能完成整体的排序。

两边的排序操作也和前面的一样。首先来看看如何对右边的数据进行排序吧。

随机选择一个基准值。这次选择6。

把其余数据分别和基准值6 进行比较，小于基准值的就往左移，大于的就往右移。完成了大小比较和位置移动。

和前面一样，对左右两边分别进行排序，进而完成整体排序。但是此时左边只有5，所以已经是排序完成的状态，不需要任何操作。而右边就和前面一样，先选出基准值。

选择8 作为基准值。将9和7分别与基准值8进行比较后，两个数字的位置便分好了。8的两边都只有一个数据，因此不需要任何操作。这样7、8、9便完成排序了。

回到上一行，由于7、8、9 完成了排序，所以5、6、7、8、9 也完成了排序。

于是，最初选择的基准值4 的右边排序完毕。

左边也以相同的操作进行排序，整体的排序工作也就完成了。

快速排序是一种“分治法”。它将原本的问题分成两个子问题（比基准值小的数和比基准值大的数），然后再分别解决这两个问题。子问题，也就是子序列完成排序后，再像一开始说明的那样，把他们合并成一个序列，那么对原始序列的排序也就完成了。
分割子序列时需要选择基准值，如果每次选择的基准值都能使得两个子序列的长度为原本的一半，那么快速排序的运行时间和归并排序的一样，都为O(nlogn)。如果运气不好，每次都选择最小值作为基准值，那么每次都需要把其他数据移到基准值的右边，递归执行n 行，运行时间也就成了 $O(n^2)$。

1

1