5793: 学习系列——二叉查找树
[Creator : ]
Description
二叉查找树(又叫作二叉搜索树或二叉排序树)是一种数据结构,采用了树形结构。数据存储于二叉查找树的各个结点中。
如果结点数为n,而且树的形状又较为均衡的话,比较大小和移动的次数最多就是log2n。因此,时间复杂度为O(logn)。但是,如果树的形状朝单侧纵向延伸,树就会变得很高,此时时间复杂度也就变成了O(n)。
【样例】
这就是二叉查找树的示例。结点中的数字便是存储的数据。此处以不存在相同数字为前提进行说明。
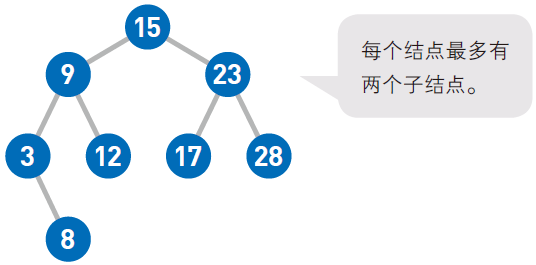
二叉查找树有两个性质。第一个是每个结点的值均大于其左子树上任意一个结点的值。比如结点9 大于其左子树上的3 和8。
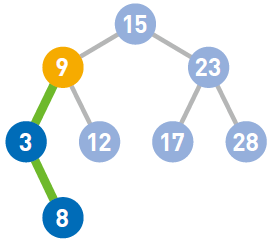
同样,结点15 也大于其左子树上任意一个结点的值。
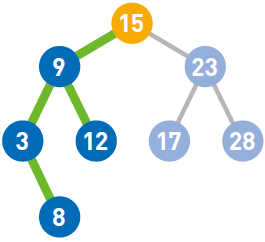
第二个是每个结点的值均小于其右子树上任意一个结点的值。比如结点15 小于其右子树上的23、17 和28。
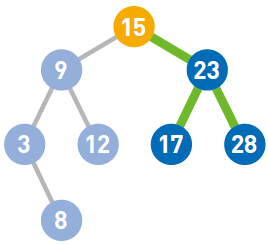
根据这两个性质可以得到以下结论。首先,二叉查找树的最小结点要从顶端开始,往其左下的末端寻找。此处最小值为3。
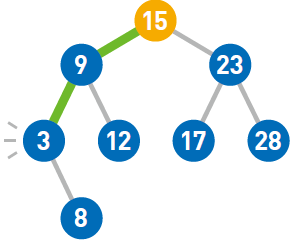
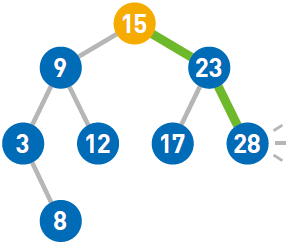
反过来,二叉查找树的最大结点要从顶端开始,往其右下的末端寻找。此处最大值为28。
【插入数据】
下面我们来试着往二叉查找树中添加数据。比如添加数字1。
首先,从二叉查找树的顶端结点开始寻找添加数字的位置。将想要添加的1与该结点中的值进行比较,小于它则往左移,大于它则往右移。
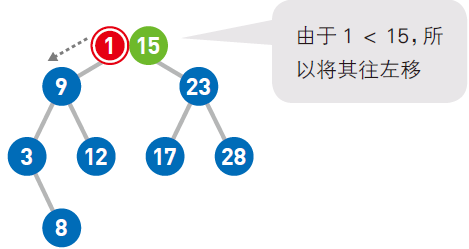
由于1 < 9,所以将1 往左移。
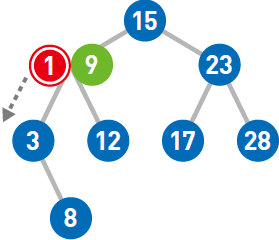
由于1<3,所以继续将1往左移,但前面已经没有结点了,所以把1 作为新结点添加到左下方。
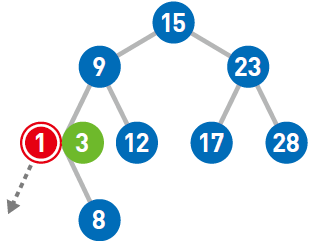
这样,1 的添加操作便完成了。
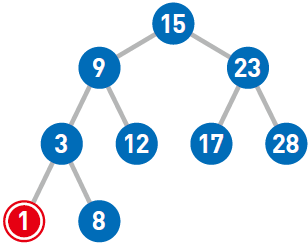
接下来,我们再试试添加数字4。
和前面的步骤一样,首先从二叉查找树的顶端结点开始寻找添加数字的位置。
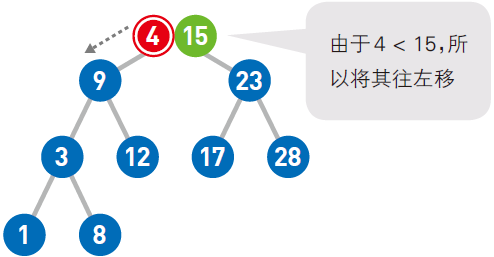
由于4 < 9,所以将其往左移。

由于4 > 3,所以将其往右移。
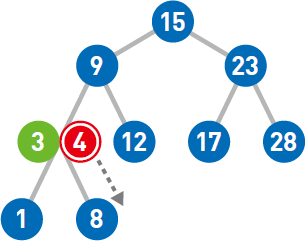
由于4<8,所以需要将其往左移,但前面已经没有结点了,所以把4 作为新结点添加到左下方。
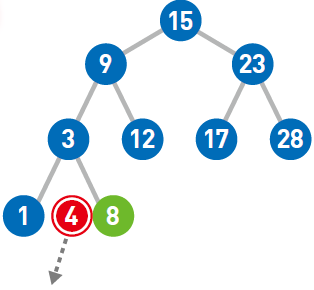
于是4 的添加操作也完成了。
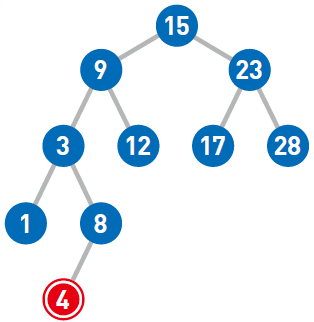
【删除】
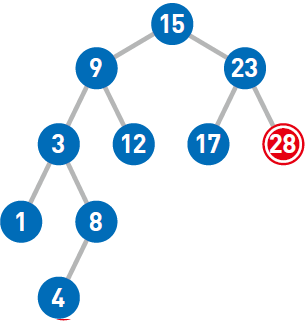
接下来看看如何在二叉查找树中删除结点。比如我们来试试删除结点28。
如果需要删除的结点没有子结点,直接删掉该结点即可。
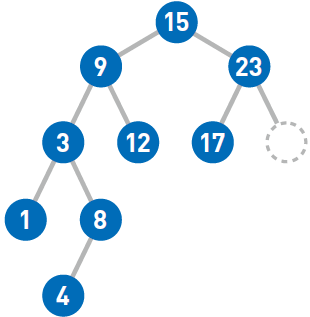
再试试删除结点8。如果需要删除的结点只有一个子结点,那么先删掉目标结点……然后把子结点移到被删除结点的位置上即可。
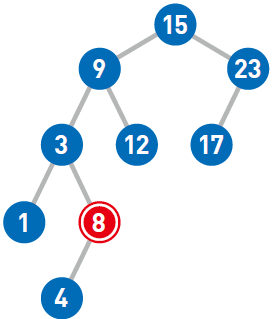
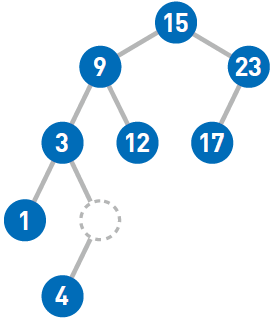
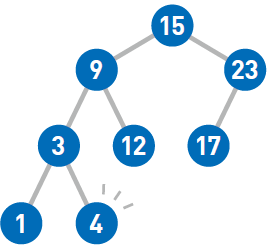
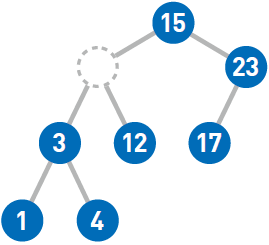
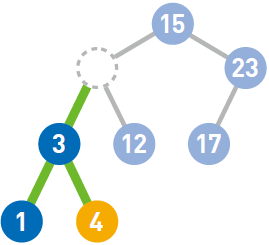
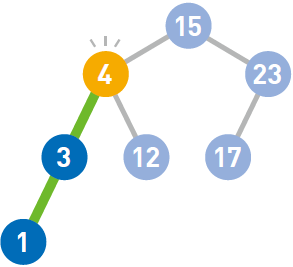
最后来试试删除结点9。如果需要删除的结点有两个子结点,那么先删掉目标结点……然后在被删除结点的左子树中寻找最大结点……最后将最大结点移到被删除结点的位置上。这样一来,就能在满足二叉查找树性质的前提下删除结点了。如果需要移动的结点(此处为4)还有子结点,就递归执行前面的操作。
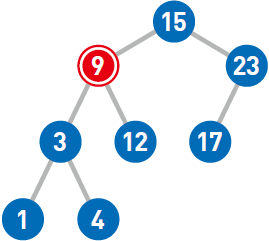
【查找】
下面来看看如何在二叉查找树中查找结点。比如我们来试试查找12。
从二叉查找树的顶端结点开始往下查找。和添加数据时一样,把12 和结点中的值进行比较,小于该结点的值则往左移,大于则往右移。
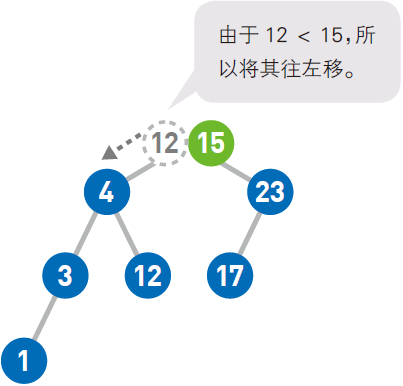
由于12 > 4,所以往右移。
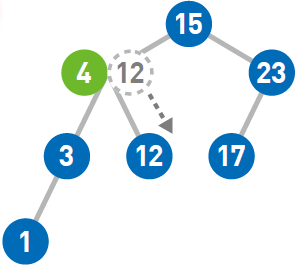
找到结点12 了。
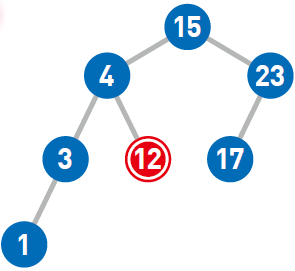
如果结点数为n,而且树的形状又较为均衡的话,比较大小和移动的次数最多就是log2n。因此,时间复杂度为O(logn)。但是,如果树的形状朝单侧纵向延伸,树就会变得很高,此时时间复杂度也就变成了O(n)。
【样例】
这就是二叉查找树的示例。结点中的数字便是存储的数据。此处以不存在相同数字为前提进行说明。

二叉查找树有两个性质。第一个是每个结点的值均大于其左子树上任意一个结点的值。比如结点9 大于其左子树上的3 和8。

同样,结点15 也大于其左子树上任意一个结点的值。

第二个是每个结点的值均小于其右子树上任意一个结点的值。比如结点15 小于其右子树上的23、17 和28。

根据这两个性质可以得到以下结论。首先,二叉查找树的最小结点要从顶端开始,往其左下的末端寻找。此处最小值为3。

反过来,二叉查找树的最大结点要从顶端开始,往其右下的末端寻找。此处最大值为28。

【插入数据】
下面我们来试着往二叉查找树中添加数据。比如添加数字1。
首先,从二叉查找树的顶端结点开始寻找添加数字的位置。将想要添加的1与该结点中的值进行比较,小于它则往左移,大于它则往右移。

由于1 < 9,所以将1 往左移。

由于1<3,所以继续将1往左移,但前面已经没有结点了,所以把1 作为新结点添加到左下方。

这样,1 的添加操作便完成了。

接下来,我们再试试添加数字4。
和前面的步骤一样,首先从二叉查找树的顶端结点开始寻找添加数字的位置。

由于4 < 9,所以将其往左移。

由于4 > 3,所以将其往右移。

由于4<8,所以需要将其往左移,但前面已经没有结点了,所以把4 作为新结点添加到左下方。

于是4 的添加操作也完成了。

【删除】
接下来看看如何在二叉查找树中删除结点。比如我们来试试删除结点28。
如果需要删除的结点没有子结点,直接删掉该结点即可。


再试试删除结点8。如果需要删除的结点只有一个子结点,那么先删掉目标结点……然后把子结点移到被删除结点的位置上即可。



最后来试试删除结点9。如果需要删除的结点有两个子结点,那么先删掉目标结点……然后在被删除结点的左子树中寻找最大结点……最后将最大结点移到被删除结点的位置上。这样一来,就能在满足二叉查找树性质的前提下删除结点了。如果需要移动的结点(此处为4)还有子结点,就递归执行前面的操作。




【查找】
下面来看看如何在二叉查找树中查找结点。比如我们来试试查找12。
从二叉查找树的顶端结点开始往下查找。和添加数据时一样,把12 和结点中的值进行比较,小于该结点的值则往左移,大于则往右移。

由于12 > 4,所以往右移。

找到结点12 了。
