5792: 学习系列——链表 I——单向链表
[Creator : ]
Description
【知识点】
链表是数据结构之一,其中的数据呈线性排列。在链表中,数据的添加和删除都较为方便,就是访问比较耗费时间。
我们把链表中的数据量记成 $n$。访问数据时,我们需要从链表头部开始查找(线性查找),如果目标数据在链表最后的话,需要的时间就是 $O(n)$。
另外,添加数据只需要更改两个指针的指向,所以耗费的时间与 $n$ 无关。如果已经到达了添加数据的位置,那么添加操作只需花费 $O(1)$ 的时间。删除数据同样也只需 $O(1)$ 的时间。
【什么是链表】
链表 是由一个个 结点 组成,每个 结点 之间通过 链接关系 串联起来,每个 结点 都有一个 后继节点,最后一个 结点 的 后继结点 为 空结点。如下图所示:
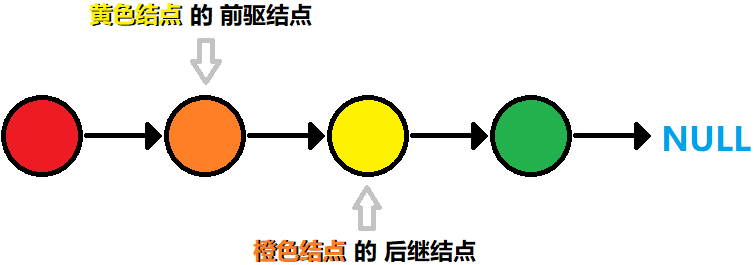
一个结点包含的两部分如下图所示:
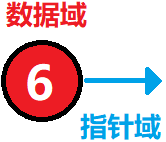

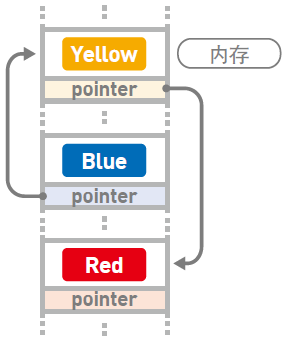
这就是链表的概念图。Blue、Yellow、Red 这 $3$ 个字符串作为数据被存储于链表中。每个数据都有 $1$ 个“指针”,它指向下一个数据的内存地址。
在链表中,数据一般都是分散存储于内存中的,无须存储在连续空间内。
【顺序访问】
因为数据都是分散存储的,所以如果想要访问数据,只能从第 $1$ 个数据开始,顺着指针的指向一一往下访问(这便是顺序访问)。比如,想要找到 Red 这一数据,就得从 Blue 开始访问。这之后,还要经过 Yellow,我们才能找到 Red。
【添加数据】
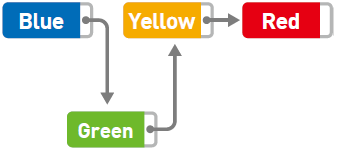
如果想要添加数据,只需要改变添加位置前后的指针指向就可以,非常简单。比如,在 Blue 和 Yellow 之间添加 Green。
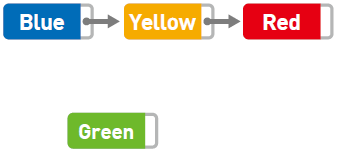
将 Blue 的指针指向的位置变成 Green,然后再把 Green 的指针指向 Yellow,数据的添加就大功告成了。
尾插法

头插法

【删除】
数据的删除也一样,只要改变指针的指向就可以,比如删除 Yellow。
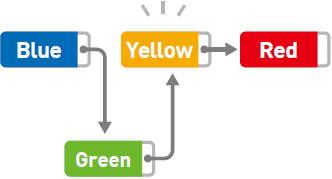
这时,只需要把 Green 指针指向的位置从 Yellow 变成 Red,删除就完成了。虽然 Yellow 本身还存储在内存中,但是不管从哪里都无法访问这个数据,所以也就没有特意去删除它的必要了。今后需要用到 Yellow 所在的存储空间时,只要用新数据覆盖掉就可以了。
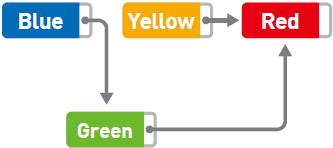
【单向链表实现】
在真正使用的时候,我们会在链表前面加上一个头结点,该结点用于表示单向链表的头位置。
对于单项链表,实现方法有两种。
【STL 的 list】
【数组模拟】
和 STL 的 list 类相比,使用数组模拟链表速度更快,但是代码量不大。这点代价我们还是可以接受的。
使用一个一维数组来模拟链表,注意元素只是增加不会减少。所以定义 MAXN 的时候需要使用 $2$ 倍的容量。
需要实现的操作有插入元素,删除元素。
【链表的定义】
在单向链表中插入元素,可以在头结点位置插入,也可以在指定的 $pos$ 位置插入。
【删除元素】
删除指定 $pos$ 位置后面的数据。
【遍历链表】
这样,我们就实现了使用数组模拟链表。
【任务】
给定一个 $N$ 次操作,每次操作为下列操作之一。
操作 $1\ x$:表示向链表头插入一个数 $x$。
操作 $2\ k$:表示删除第 $k$ 个位置的后面的数(当 $k$ 为 $0$ 时,表示删除头结点)。
操作 $3\ k\ x$:表示在第 $k$ 个位置的后面插入一个数 $x$(此操作中 $k$ 均大于 $0$)。
链表是数据结构之一,其中的数据呈线性排列。在链表中,数据的添加和删除都较为方便,就是访问比较耗费时间。
我们把链表中的数据量记成 $n$。访问数据时,我们需要从链表头部开始查找(线性查找),如果目标数据在链表最后的话,需要的时间就是 $O(n)$。
另外,添加数据只需要更改两个指针的指向,所以耗费的时间与 $n$ 无关。如果已经到达了添加数据的位置,那么添加操作只需花费 $O(1)$ 的时间。删除数据同样也只需 $O(1)$ 的时间。
【什么是链表】
链表 是由一个个 结点 组成,每个 结点 之间通过 链接关系 串联起来,每个 结点 都有一个 后继节点,最后一个 结点 的 后继结点 为 空结点。如下图所示:

一个结点包含的两部分如下图所示:


这就是链表的概念图。Blue、Yellow、Red 这 $3$ 个字符串作为数据被存储于链表中。每个数据都有 $1$ 个“指针”,它指向下一个数据的内存地址。
在链表中,数据一般都是分散存储于内存中的,无须存储在连续空间内。

【顺序访问】
因为数据都是分散存储的,所以如果想要访问数据,只能从第 $1$ 个数据开始,顺着指针的指向一一往下访问(这便是顺序访问)。比如,想要找到 Red 这一数据,就得从 Blue 开始访问。这之后,还要经过 Yellow,我们才能找到 Red。
【添加数据】
如果想要添加数据,只需要改变添加位置前后的指针指向就可以,非常简单。比如,在 Blue 和 Yellow 之间添加 Green。

将 Blue 的指针指向的位置变成 Green,然后再把 Green 的指针指向 Yellow,数据的添加就大功告成了。

尾插法

头插法

【删除】
数据的删除也一样,只要改变指针的指向就可以,比如删除 Yellow。

这时,只需要把 Green 指针指向的位置从 Yellow 变成 Red,删除就完成了。虽然 Yellow 本身还存储在内存中,但是不管从哪里都无法访问这个数据,所以也就没有特意去删除它的必要了。今后需要用到 Yellow 所在的存储空间时,只要用新数据覆盖掉就可以了。

【单向链表实现】
在真正使用的时候,我们会在链表前面加上一个头结点,该结点用于表示单向链表的头位置。
对于单项链表,实现方法有两种。
【STL 的 list】
【数组模拟】
和 STL 的 list 类相比,使用数组模拟链表速度更快,但是代码量不大。这点代价我们还是可以接受的。
使用一个一维数组来模拟链表,注意元素只是增加不会减少。所以定义 MAXN 的时候需要使用 $2$ 倍的容量。
需要实现的操作有插入元素,删除元素。
【链表的定义】
const int MAXN=2e6+10; //数组元素个数 LL e[MAXN]; //保存链表的结点。e[i] 表示第 i 个链表的数据为 e[i] LL ne[MAXN]; //保存链表的下一个结点索引。ne[i] 表示第 i 个链表的下一个结点为 ne[i],其中 ne[0] 保存头结点位置 LL idx; //用到数组的索引。【链表的初始化】
void init() {
ne[0]=-1;//头结点
idx=1; //链表头结点已经使用
}
【插入元素】 在单向链表中插入元素,可以在头结点位置插入,也可以在指定的 $pos$ 位置插入。
void add(LL val, LL pos=-1) {
e[idx]=val;//插入数据
if (pos<0) {
//插入头结点
ne[idx]=ne[0];//修改指针
ne[0]=idx++;//长度增加
} else {
//插入到pos位置
ne[idx]=ne[pos];
ne[pos]=idx++;
}
}
【删除元素】
删除指定 $pos$ 位置后面的数据。
void remove(LL pos) {
ne[pos]=ne[ne[pos]];//删除指针
}
【遍历链表】
//遍历链表
for (LL i=ne[0]; i!=-1; i=ne[i]) {
cout<<e[i]<<" ";
}
cout<<"\n";
这样,我们就实现了使用数组模拟链表。
【任务】
给定一个 $N$ 次操作,每次操作为下列操作之一。
操作 $1\ x$:表示向链表头插入一个数 $x$。
操作 $2\ k$:表示删除第 $k$ 个位置的后面的数(当 $k$ 为 $0$ 时,表示删除头结点)。
操作 $3\ k\ x$:表示在第 $k$ 个位置的后面插入一个数 $x$(此操作中 $k$ 均大于 $0$)。
Input
第一行两个整数 $N\ (N ≤ 1,000)$,含义见试题描述。
接下来 $N$ 行,表示有 $N$ 个操作,具体操作参看题目描述。
接下来 $N$ 行,表示有 $N$ 个操作,具体操作参看题目描述。
Output
输出包括 $N$ 组,每组输出包括三行。
第一行输出:op:x,其中 $x$ 表示第几次操作。具体看样例输出。
第二行若干个数,将整个链表从左到右输出。
第三行为一个空行。
第一行输出:op:x,其中 $x$ 表示第几次操作。具体看样例输出。
第二行若干个数,将整个链表从左到右输出。
第三行为一个空行。
Sample 1 Input
10
1 9
3 1 -100
2 1
2 0
1 6
3 3 65
3 4 523
3 4 -5
3 3 -4
2 6
Sample 1 Output
op:1
9
op:2
9 -100
op:3
9
op:4
op:5
6
op:6
6 65
op:7
6 65 523
op:8
6 65 -5 523
op:9
6 -4 65 -5 523
op:10
6 -4 65 -5