5760: 学习系列——ST 表 I ——区间最大值
[Creator : ]
Description
ST 表是用于解决:可重复贡献问题,区间按位和,区间按位或,区间 GCD 的数据结构。
ST 表的优点:时间复杂度较低,代码量相对其他算法很小。
ST 表的缺点:ST 表能维护的信息非常有限,不能较好地扩展,并且不支持修改操作。
【什么是可重复贡献问题】
可重复贡献问题 是指对于运算 $\text{opt}$,满足 $x \text{opt} x=x$,则对应的区间询问就是一个可重复贡献问题。例如,最大值有 $\text{max}(x, x) =x$,gcd 有 $\text{gcd}(x,x)=x$,所以 RMQ 和区间 GCD 就是一个可重复贡献问题。像区间和就不具有这个性质,如果求区间和的时候采用的预处理区间重叠了,则会导致重叠部分被计算两次,这是我们所不愿意看到的。另外,$\text{opt}$ 还必须满足结合律才能使用 ST 表求解。
【ST 表】
ST 表基于倍增思想,可以做到 $\Theta(n logn)$ 预处理,$\Theta(1)$ 回答每个询问。但是不支持修改操作。
基于倍增思想,我们考虑如何求出区间最大值。可以发现,如果按照一般的倍增流程,每次跳 $2^i$ 步的话,询问时的复杂度仍旧是 $\Theta(n)$,并没有比线段树更优,反而预处理一步还比线段树慢。
我们发现 $\text{max}(x,x)=x$,也就是说,区间最大值是一个具有“可重复贡献”性质的问题。即使用来求解的预处理区间有重叠部分,只要这些区间的并是所求的区间,最终计算出的答案就是正确的。
如果手动模拟一下,可以发现我们能使用至多两个预处理过的区间来覆盖询问区间,也就是说询问时的时间复杂度可以被降至 $\Theta(1)$,在处理有大量询问的题目时十分有效。
【ST 表实现】
ST 表的实现分为两个部分:预处理和查询。
【预处理】
令 $f(i,\ j)$ 表示区间 $[i,\ i+2^j-1]$ 的最大值。
显然 $f(i,\ 0)=a_i$。
根据定义式,第二维就相当于倍增的时候“跳了 $2^j-1$ 步”,依据倍增的思路,写出状态转移方程:$f(i,\ j)=\text{max}(f(i,\ j-1),\ f(i+2^{j-1}, j-1))$。
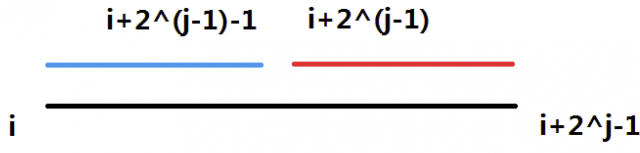
【查询】
而对于查询,可以简单实现如下:
对于每个询问 [l, r],我们把它分成两部分:f[$l, l+2^s-1$] 与 f[$r-2^s+1, r$]。
其中 $s=\lfloor log_2(r-l+1) \rfloor$。
根据上面对于“可重复贡献问题”的论证,由于最大值是“可重复贡献问题”,重叠并不会对区间最大值产生影响。又因为这两个区间完全覆盖了 $[l,\ r]$,可以保证答案的正确性。
【数据定义】
【预处理】
【查询部分】
我们需要查询区间 [l, r] 的最大值。
【注意点】 1、输入输出数据一般很多,建议开启输入输出优化。
2、每次用 std::log 重新计算 log 函数值并不值得,建议进行如下的预处理:
$\begin{equation} \left\{\begin{aligned}\text{Logn[1]}&=&0\\\text{Logn[i]}&=&\text{Logn}[\frac{i}{2}]+1 \end{aligned}\right.\end{equation}$
【什么是 RMQ】
RMQ 是英文 Range Maximum/Minimum Query 的缩写,表示区间最大(最小)值。解决 RMQ 问题有很多种方法,ST 表是其中的一个方法之一。
【问题】
给定一个长度为 $N$ 的数列,和 $M$ 次询问,求出每一次询问的区间内数字的最大值。
ST 表的优点:时间复杂度较低,代码量相对其他算法很小。
ST 表的缺点:ST 表能维护的信息非常有限,不能较好地扩展,并且不支持修改操作。
【什么是可重复贡献问题】
可重复贡献问题 是指对于运算 $\text{opt}$,满足 $x \text{opt} x=x$,则对应的区间询问就是一个可重复贡献问题。例如,最大值有 $\text{max}(x, x) =x$,gcd 有 $\text{gcd}(x,x)=x$,所以 RMQ 和区间 GCD 就是一个可重复贡献问题。像区间和就不具有这个性质,如果求区间和的时候采用的预处理区间重叠了,则会导致重叠部分被计算两次,这是我们所不愿意看到的。另外,$\text{opt}$ 还必须满足结合律才能使用 ST 表求解。
【ST 表】
ST 表基于倍增思想,可以做到 $\Theta(n logn)$ 预处理,$\Theta(1)$ 回答每个询问。但是不支持修改操作。
基于倍增思想,我们考虑如何求出区间最大值。可以发现,如果按照一般的倍增流程,每次跳 $2^i$ 步的话,询问时的复杂度仍旧是 $\Theta(n)$,并没有比线段树更优,反而预处理一步还比线段树慢。
我们发现 $\text{max}(x,x)=x$,也就是说,区间最大值是一个具有“可重复贡献”性质的问题。即使用来求解的预处理区间有重叠部分,只要这些区间的并是所求的区间,最终计算出的答案就是正确的。
如果手动模拟一下,可以发现我们能使用至多两个预处理过的区间来覆盖询问区间,也就是说询问时的时间复杂度可以被降至 $\Theta(1)$,在处理有大量询问的题目时十分有效。
【ST 表实现】
ST 表的实现分为两个部分:预处理和查询。
【预处理】
令 $f(i,\ j)$ 表示区间 $[i,\ i+2^j-1]$ 的最大值。
显然 $f(i,\ 0)=a_i$。
根据定义式,第二维就相当于倍增的时候“跳了 $2^j-1$ 步”,依据倍增的思路,写出状态转移方程:$f(i,\ j)=\text{max}(f(i,\ j-1),\ f(i+2^{j-1}, j-1))$。
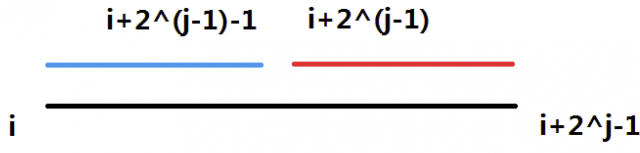
【查询】
而对于查询,可以简单实现如下:
对于每个询问 [l, r],我们把它分成两部分:f[$l, l+2^s-1$] 与 f[$r-2^s+1, r$]。
其中 $s=\lfloor log_2(r-l+1) \rfloor$。
根据上面对于“可重复贡献问题”的论证,由于最大值是“可重复贡献问题”,重叠并不会对区间最大值产生影响。又因为这两个区间完全覆盖了 $[l,\ r]$,可以保证答案的正确性。
【数据定义】
const int MAXN=2e6+10; const int LOGN=24; LL Logn[MAXN];//预处理 LL f[MAXN][LOGN];
【预处理】
//准备工作,初始化
Logn[1]=0;
Logn[2]=1;
for (LL i=3; i<MAXN; i++) {
Logn[i]=Logn[i/2]+1;
}
// ST表具体实现
for (int j=1; j<=LOGN; j++) {
for(int i=1; i+(1<<j)-1<=n; i++) {
f[i][j]=max(f[i][j-1], f[i+(1<<(j-1))][j-1]);
}
}
【查询部分】
我们需要查询区间 [l, r] 的最大值。
LL s=Logn[r-l+1]; LL ans=max(f[l], f[y-(1<<s)+1]);
【注意点】 1、输入输出数据一般很多,建议开启输入输出优化。
2、每次用 std::log 重新计算 log 函数值并不值得,建议进行如下的预处理:
$\begin{equation} \left\{\begin{aligned}\text{Logn[1]}&=&0\\\text{Logn[i]}&=&\text{Logn}[\frac{i}{2}]+1 \end{aligned}\right.\end{equation}$
【什么是 RMQ】
RMQ 是英文 Range Maximum/Minimum Query 的缩写,表示区间最大(最小)值。解决 RMQ 问题有很多种方法,ST 表是其中的一个方法之一。
【问题】
给定一个长度为 $N$ 的数列,和 $M$ 次询问,求出每一次询问的区间内数字的最大值。
Input
第一行包含两个整数 $N,\ M$,分别表示数列的长度和询问的个数。
第二行包含 $N$ 个整数(记为 $a_i$),依次表示数列的第 $i$ 项。
接下来 $M$ 行,每行包含两个整数 $l_i,\ r_i$,表示查询的区间为 $[l_i,\ r_i]$。
第二行包含 $N$ 个整数(记为 $a_i$),依次表示数列的第 $i$ 项。
接下来 $M$ 行,每行包含两个整数 $l_i,\ r_i$,表示查询的区间为 $[l_i,\ r_i]$。
Output
输出包含 $M$ 行,每行一个整数,依次表示每一次询问的结果。
Constraints
对于 $30\%$ 的数据,满足 $1\le N,\ M\le 10$。
对于 $70\%$ 的数据,满足 $1\le N,\ M\le {10}^5$。
对于 $100\%$ 的数据,满足 $1\le N\le {10}^5,\ 1\le M\le 2\times{10}^6,\ a_i\in [0,\ {10}^9],\ 1\le l_i\le r_i\le N$。
对于 $70\%$ 的数据,满足 $1\le N,\ M\le {10}^5$。
对于 $100\%$ 的数据,满足 $1\le N\le {10}^5,\ 1\le M\le 2\times{10}^6,\ a_i\in [0,\ {10}^9],\ 1\le l_i\le r_i\le N$。
Sample 1 Input
8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8
Sample 1 Output
9
9
7
7
9
8
7
9