哈希表存储的是由键（key）和值（value）组成的数据。
【问题】
例如，我们将每个人的性别作为数据进行存储，键为人名，值为对应的性别。

【使用数组保存】
为了和哈希表进行对比，我们先将这些数据存储在数组中。

此处准备了6 个箱子（即长度为6 的数组）来存储数据。假设我们需要查询Ally 的性别，由于不知道Ally 的数据存储在哪个箱子里，所以只能从头开始查询。这个操作便叫作“线性查找”。

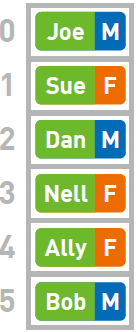
0 号箱子中存储的键是Joe 而不是Ally。1 号箱子中的也不是Ally。同样，2 号、3 号箱子中的也都不是Ally。查找到4 号箱子的时候，发现其中数据的键为Ally。把键对应的值取出，我们就知道Ally 的性别为女（F）了。
数据量越多，线性查找耗费的时间就越长。由此可知：由于数据的查询较为耗时，所以此处并不适合使用数组来存储数据。
【哈希表】
但使用哈希表便可以解决这个问题。首先准备好数组，这次我们用5 个箱子的数组来存储数据。

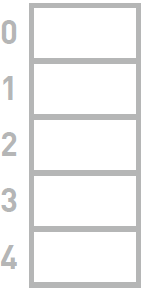
尝试把Joe 存进去。使用哈希函数（Hash）计算Joe 的键，也就是字符串“Joe”的哈希值。得到的结果为4928。将得到的哈希值除以数组的长度5，求得其余数。这样的求余运算叫作“mod 运算”。此处mod 运算的结果为3。因此，我们将Joe 的数据存进数组的3 号箱子中。重复前面的操作，将其他数据也存进数组中。

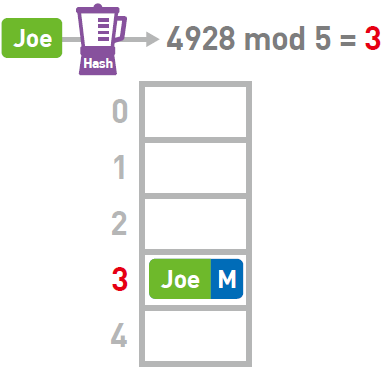
Sue 键的哈希值为7291，mod 5 的结果为1，将Sue 的数据存进1 号箱中。
Dan 键的哈希值为1539，mod 5 的结果为4，将Dan 的数据存进4 号箱中。

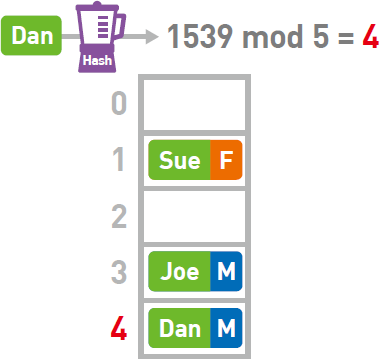
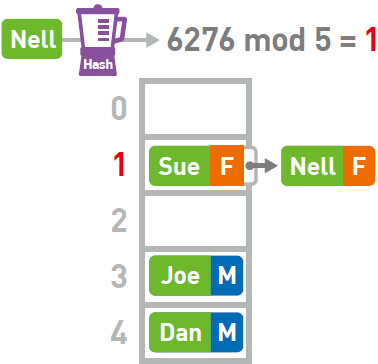
Nell 键的哈希值为6276，mod 5 的结果为1。本应将其存进数组的1 号箱中，但此时1 号箱中已经存储了Sue 的数据。这种存储位置重复了的情况便叫作“冲突”。

遇到这种情况，可使用链表在已有数据的后面继续存储新的数据。

Ally 键的哈希值为9143，mod 5 的结果为3。本应将其存储在数组的3 号箱中，但3 号箱中已经有了Joe 的数据，所以使用链表，在其后面存储Ally 的数据。
Bob 键的哈希值为5278，mod 5 的结果为3。本应将其存储在数组的3 号箱中，但3 号箱中已经有了Joe 和Ally 的数据，所以使用链表，在Ally 的后面继续存储Bob 的数据。

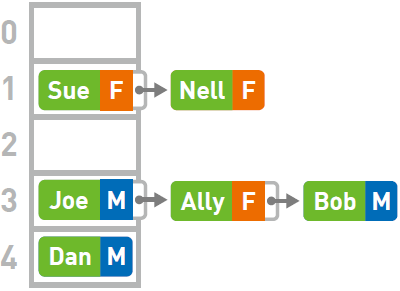
像这样存储完所有数据，哈希表也就制作完成了。
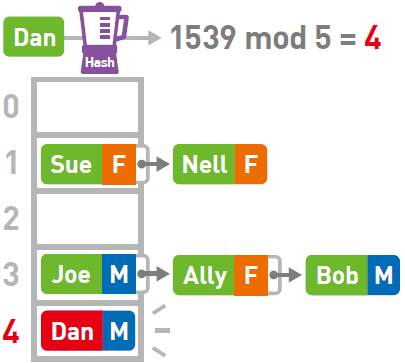
接下来讲解数据的查询方法。假设我们要查询Dan 的性别。为了知道Dan存储在哪个箱子里，首先需要算出Dan键的哈希值，然后对其进行mod运算。最后得到的结果为4，于是我们知道了它存储在4号箱中。查看4 号箱可知，其中的数据的键与Dan 一致，于是取出对应的值。由此我们便知道了Dan 的性别为男（M）。

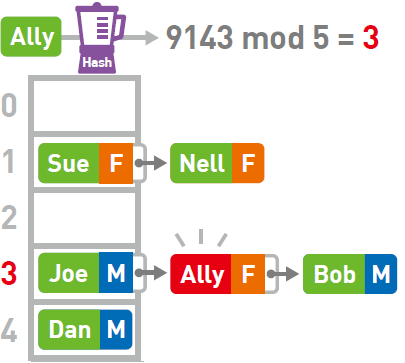
那么，想要查询Ally 的性别时该怎么做呢？为了找到它的存储位置，先要算出Ally键的哈希值，再对其进行mod运算。最终得到的结果为3。然而3 号箱中数据的键是Joe 而不是Ally。此时便需要对Joe 所在的链表进行线性查找。于是我们找到了键为Ally 的数据。取出其对应的值，便知道了Ally 的性别为女（F）。

第一行包含整数 $n\ (1≤n≤10^5)$，表示有 $n$ 字符串，每个字符串的长度不会超过 $256$。
第二行到 $n+1$ 行，每行包含一个字符串 $s1$。第 $i$ 行表示字符串 $s1$ 出现了一次。
第 $n+2$ 行，一个整数 $m\ (1≤m≤10^5)$，表示有 $m$ 次询问。
接下来 $m$ 行，每行包含一个字符串 $s2$，表示询问 $s2$ 出现的次数。

一共 $m$ 行，每行一个整数，输出询问字符串出现的次数。