【知识点】
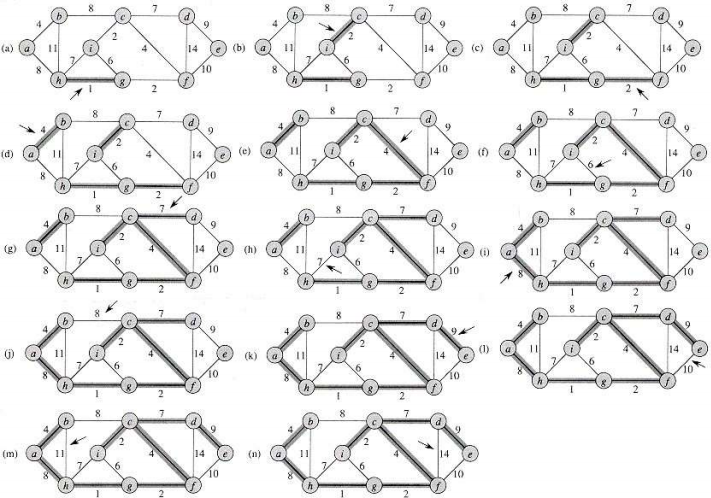
Kruskal 算法是增对图的边进行，依次在两颗生成树间加入一条权值最小的边。
因此算法的时间复杂度为 $O(mlogm)$，适用与稀疏图，即 $m<n^2$。



【问题】
给定一个 $n$ 个点 $m$ 条边的无向图，图中可能存在重边和自环，边权可能为负数。
求最小生成树的树边权重之和，如果最小生成树不存在则输出 ${impossible}$。
给定一张边带权的无向图 $G=(V,\ E)$，其中 $V$ 表示图中点的集合，$E$ 表示图中边的集合，$n=|V|,\ m=|E|$。
由 $V$ 中的全部 $n$ 个顶点和 $E$ 中 $n−1$ 条边构成的无向连通子图被称为 $G$ 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 $G$ 的最小生成树。

第一行包含两个整数 $n$ 和 $m$。
接下来 $m$ 行，每行包含三个整数 $u,\ v,\ w$，表示点 $u$ 和点 $v$ 之间存在一条权值为 $w$ 的边。

共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 ${impossible}$。

$1≤n≤10^5$,
$1≤m≤2∗10^5$,
图中涉及边的边权的绝对值均不超过 $1,000$。