5644: ABC181——F - Silver Woods
[Creator : ]
Description
On the $xy$-plane, we have a passage surrounded by the two lines $y=-100$ and $y=100$.
In the part of this passage with $-100<x<100$, there are $N$ negligibly small nails. The coordinates of the $i$-th nail are $(x_i,\ y_i)$.
Takahashi will choose a real number $r\ (0<r≤100)$ and put a circle of radius $r$ so that its center is at $(-10^9,\ 0)$.
Then, he will move the circle from $(-10^9,\ 0)$ to $(10^9,\ 0)$.
Here, he continuously moves the circle so that the boundaries of the passage or the nails do not penetrate the interior of the circle.
Find the maximum possible value of $r$ such that it is possible to move the circle to $(10^9,\ 0)$.
In the part of this passage with $-100<x<100$, there are $N$ negligibly small nails. The coordinates of the $i$-th nail are $(x_i,\ y_i)$.
Takahashi will choose a real number $r\ (0<r≤100)$ and put a circle of radius $r$ so that its center is at $(-10^9,\ 0)$.
Then, he will move the circle from $(-10^9,\ 0)$ to $(10^9,\ 0)$.
Here, he continuously moves the circle so that the boundaries of the passage or the nails do not penetrate the interior of the circle.
Find the maximum possible value of $r$ such that it is possible to move the circle to $(10^9,\ 0)$.
Input
Input is given from Standard Input in the following format:
$N$
$x_1\ y_1$
$\dots$
$x_N\ y_N$
$N$
$x_1\ y_1$
$\dots$
$x_N\ y_N$
Output
Print the maximum possible value of $r$ such that it is possible to move the circle to $(10^9,\ 0)$. Your output will be considered correct when its absolute or relative error from our answer is at most $10^{-4}$.
Constraints
All values in input are integers.
$1≤N≤100$
$|x_i|,\ |y_i|<100$
If $i≠j,\ (x_i,\ y_i)≠(x_j,\ y_j)$.
$1≤N≤100$
$|x_i|,\ |y_i|<100$
If $i≠j,\ (x_i,\ y_i)≠(x_j,\ y_j)$.
Sample 1 Input
2
0 -40
0 40
Sample 1 Output
40
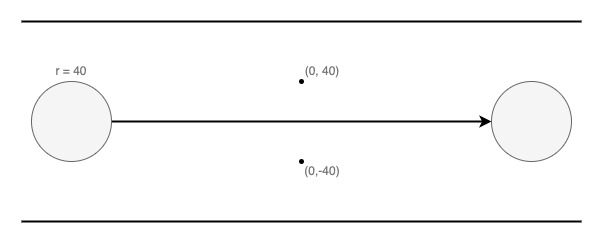
As shown in the figure, we can move the circle with $r=40$ from $(-10^9,\ 0)$ to $(10^9,\ 0)$ by moving it along $y=0$.
When $x=0$, the circle exactly touches the two nails, which is fine since they do not penetrate the interior of the circle.
Any value of $r$ greater than $40$ makes it impossible to move the circle to $(10^9,\ 0)$, so the maximum possible value is $r=40$.
Sample 2 Input
4
0 -10
99 10
0 91
99 -91
Sample 2 Output
50.5
Sample 3 Input
10
-90 40
20 -30
0 -90
10 -70
80 70
-90 30
-20 -80
10 90
50 30
60 -70
Sample 3 Output
33.541019662496845446