DreamGrid is climbing a mountain. The mountain is described by a polyline on a 2D plane:
$$(0, 0) - (1, h_1) - (2, h_2) - \cdots - (n, h_n) - (n+1, 0)$$
The region surrounded by the polyline and the x-axis denotes the mountain.
DreamGrid takes $n$ pictures at the points $(i, h_i)$ for each integer $i$ where $1 \le i \le n$. A picture covers a rectangle on the plane. Formally, a picture taken at $(i, h_i)$ covers all the points $(x, y)$ where $i - W \le x \le i + W$ and $h_i - H \le y \le h_i + H$.
However, his hard disk has limited space. When he saves the pictures into his hard disk, he can keep only $K$ pictures. He wants to maximize the total area of the mountain which is covered by at least one picture. You are asked to find the maximum area for $K = 1,\ 2,\ \cdots,\ n$.

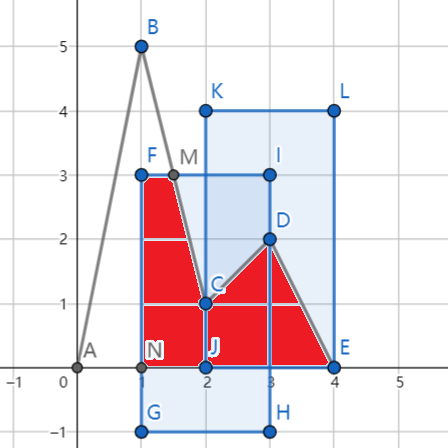
The graph above is a sample where $n = 3, W = 1, H = 2$. The polyline describing the mountain is A-B-C-D-E. DreamGrid keeps $2$ pictures taken at C and D. The red area (polygon F-M-C-D-E-N-F) is the part of the mountain covered by the kept pictures.

The first line of the input contains three integers $n, W$ and $H$ ($1 \le n \le 200$, $1 \le W \le 5$, $1 \le H \le 10\,000$), indicating the number of points on the polyline and the size of the pictures.

The second line contains $n$ integers $h_1, h_2, \cdots, h_n$ ($1 \le h_i \le 10\,000$), indicating the $y$ coordinates of the $n$ points on the polyline.

Output $n$ lines, the $i$-th line contains a float number indicating the maximum area when $K = i$.

Your answer is acceptable if its absolute or relative error does not exceed $10^{-6}$.

Formally speaking, suppose that your output is $x$ and the jury's answer is $y$. Your output is accepted if and only if $\frac{|x - y|}{\max(1, |y|)} \leq 10^{-6}$.