5551: 山峰和旗子
[Creator : ]
Description
用一个长度为 $N$ 的整数数组 A,描述山峰和山谷的高度。山峰需要满足如下条件,$0 < P < N - 1$ 且 $A[P - 1] < A[P] > A[P + 1]$。
现在要在山峰上插上 $K$ 个旗子,并且每个旗子之间的距离 $\ge K$,问最多能插上多少个旗子(即求 $K$ 的最大值)。两个山峰之间的距离为 $|P - Q|$。
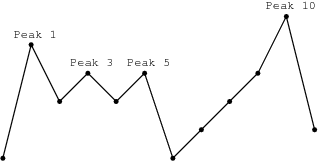
以上图为例,山峰高度为:$1\ 5\ 3\ 4\ 3\ 4\ 1\ 2\ 3\ 4\ 6\ 2$。其中可以作为山峰的点为:$1\ 3\ 5\ 10$。
放 $2$ 面旗子, 可以放在 $1$ 和 $5$。
放 $3$ 面旗子, 可以放在 $1\ 5$ 和 $10$。
放 $4$ 面旗子, 可以放在 $1\ 5$ 和 $10$,之后就放不下了。
所以最多可以放 $3$ 面旗子。
现在要在山峰上插上 $K$ 个旗子,并且每个旗子之间的距离 $\ge K$,问最多能插上多少个旗子(即求 $K$ 的最大值)。两个山峰之间的距离为 $|P - Q|$。

以上图为例,山峰高度为:$1\ 5\ 3\ 4\ 3\ 4\ 1\ 2\ 3\ 4\ 6\ 2$。其中可以作为山峰的点为:$1\ 3\ 5\ 10$。
放 $2$ 面旗子, 可以放在 $1$ 和 $5$。
放 $3$ 面旗子, 可以放在 $1\ 5$ 和 $10$。
放 $4$ 面旗子, 可以放在 $1\ 5$ 和 $10$,之后就放不下了。
所以最多可以放 $3$ 面旗子。
Input
第一行:一个数 $N\ (1 \leq N \leq 50000)$,表示数组的长度。
第 $2$ 行:包括 $N$ 个正整数,第 $i$ 个数 $A_i\ (1 \leq A_i \leq 10^9)$ 表示第 $i$ 做山峰的高度。
第 $2$ 行:包括 $N$ 个正整数,第 $i$ 个数 $A_i\ (1 \leq A_i \leq 10^9)$ 表示第 $i$ 做山峰的高度。
Output
输出最多能插上多少面旗子(即求 $K$ 的最大值)。
Sample 1 Input
12
1 5 3 4 3 4 1 2 3 4 6 2
Sample 1 Output
3