乐乐要是开始他的背包旅行，这次共$n$ 个城市，编号为 $1$～$n$。乐乐从编号为 $1$ 的城市出发，前往编号为 $n$ 的城市。每个城市都有一件物品，重量为 $w_i$，价值为 $v_i$。
乐乐从一个城市到另一个城市，如果背包中的物品重量为 $a$，行走距离为 $b$ 时，花费的体力为 $a \times b$，乐乐最多只能背总重量为 $W$ 的物品。乐乐希望到达 $n$ 时，背包中的物品价值最大，同时花费的体力最小。
$n$ 个城市之间共 $m$ 条单向路，且无环，从一个城市出发之后，无法再回到这个城市。

第一行三个整数 $n,\ m,\ W$。
接下来 $n$ 行，每行 $2$ 个整数表示 $w_i$ 和 $v_i$。
接下来 $m$ 行，每行 $3$ 个整数 $x_i,\ y_i,\ z_i$，无重边，无子环。
数据保证 $1$ 可以到达 $n$。

输出两个整数，表示最大值价值和获得最大值情况下最小的体力消耗。

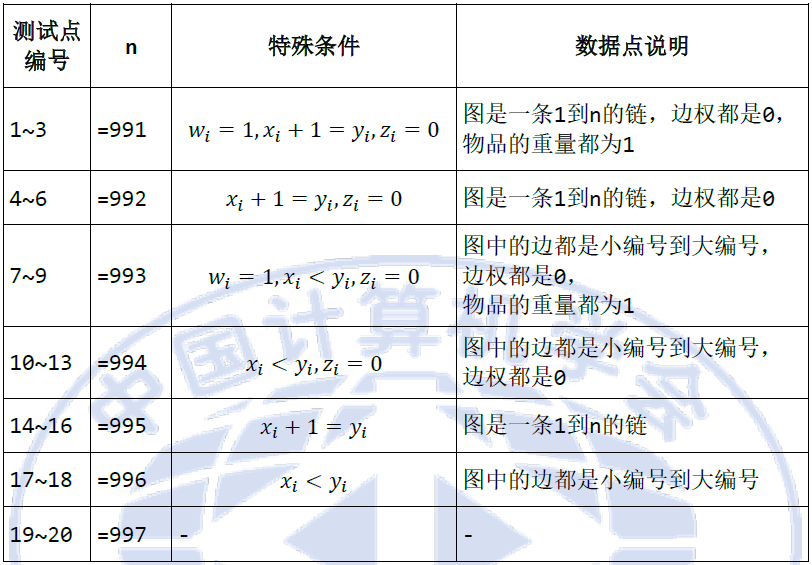
$m \leq 20000,\ W \leq 1000,\ 0 \leq z_i \leq 1000,\ 1 \leq w_i,\ v_i \leq 1000$