4660: 图
[Creator : ]
Description
在一个 $n$个节点,编号为 $1\sim n$,$n$ 条边的连通图中,每个点的权值都是正整数,每条边的权值为两个端点的权值的和。
已知各边权值,求各点权值。
已知各边权值,求各点权值。
Input
第一行一个整数 $n$。
接下来 $n$ 行,每行 $3$ 个整数 $x,y,z\ (1 \le x,y \le n)$,表示连接点 $x$ 和 $y$ 的边的权值为 $z$。
数据保证合法,且没有自环或重边。给出的图中有且只有一个包括奇数个节点的环。
接下来 $n$ 行,每行 $3$ 个整数 $x,y,z\ (1 \le x,y \le n)$,表示连接点 $x$ 和 $y$ 的边的权值为 $z$。
数据保证合法,且没有自环或重边。给出的图中有且只有一个包括奇数个节点的环。
Output
$n$ 行。每行一个正整数 $w_i$,表示点 $i$ 的权值。
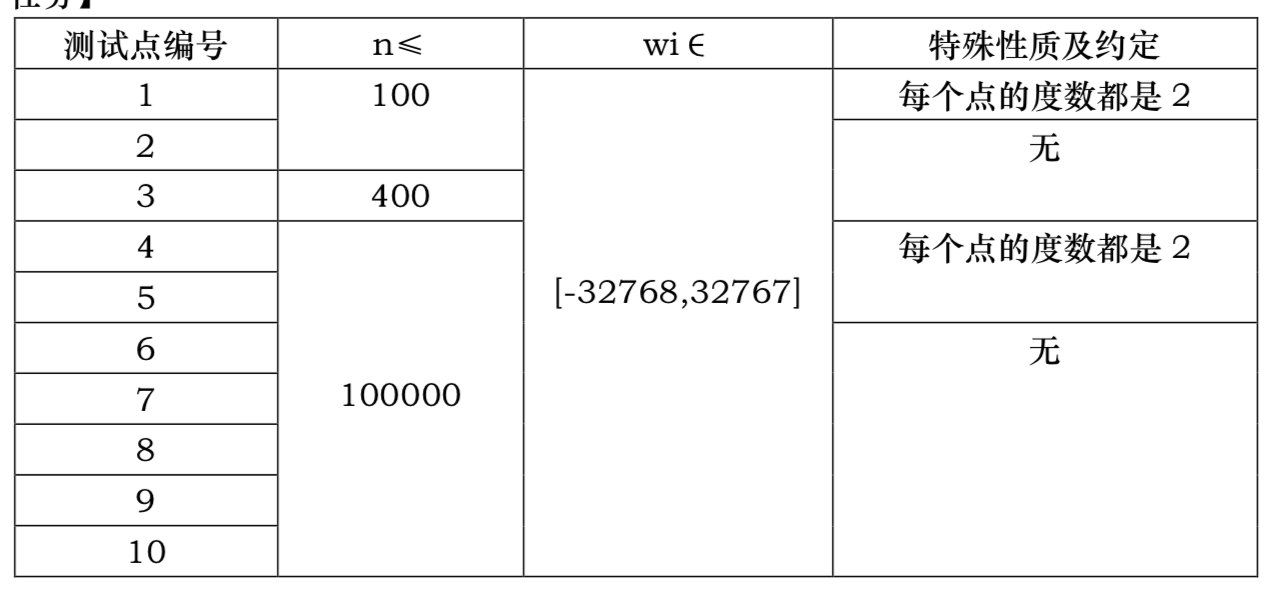
Constraints
Sample 1 Input
3
1 2 3
2 3 5
1 3 4
Sample 1 Output
1
2
3
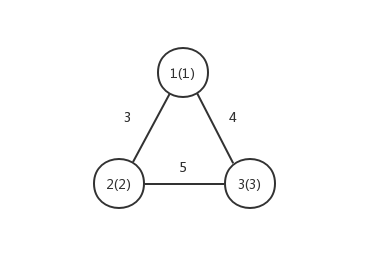
样例对应的图如下,其中括号里面的值表示点权。$1$ 号节点的点权为 $1$,$2$ 号节点的点权为 $2$,$3$ 号节点的点权为 $3$。