4171: [USACO 2010 Jan]下午茶时间
[Creator : ]
Description
$N\ (1≤N≤1000)$ 头奶牛,编号为 $1\ ..\ N$,在参加一个喝茶时间活动。
在喝茶时间活动开始之前,已经有 $M(1 \le M \le 2,000)$ 对奶牛彼此认识(是朋友)。第 $i$ 对彼此认识的奶牛通过两个不相同的整数 $A_i$ 和 $B_i$ 给定 $(1\le A_i \le N,\ 1 \le B_i \le N)$。
输入数据保证一对奶牛不会出现多次。 在喝茶时间活动中,如果奶牛 $i$ 和奶牛 $j$ 有一个相同的朋友奶牛 $k$,那么他们会在某次的喝茶活动中去认识对方(成为朋友),从而扩大他们的社交圈。
请判断,在喝茶活动举办很久以后(直到没有新的奶牛彼此认识),$Q\ (1 \le Q \le 100)$ 对奶牛是否已经彼此认识。询问 $j$ 包含一对不同的奶牛编号 $X_j,\ Y_j\ (1 \le X_j \le N,\ 1 \le Y_j \le N)$。
例如,假设共有 $1\ ..\ 5$ 头奶牛,我们知道 $2$ 号认识 $5$ 号,$2$ 号认识 $3$ 号,而且 $4$ 号认识 $5$ 号;如下图 (a)。
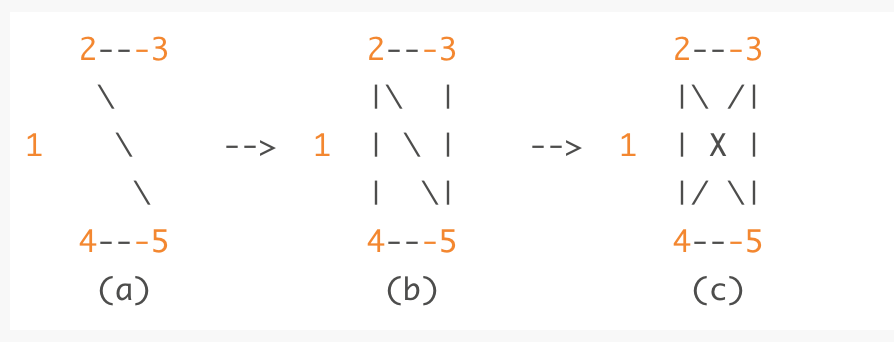
在某次的喝茶活动中,$2$ 号认识 $4$ 号,$3$ 号认识 $5$ 号;如上图(b)所示。接下来的喝茶活动中,$3$ 号认识 $4$ 号,如上图(c)所示。
在喝茶时间活动开始之前,已经有 $M(1 \le M \le 2,000)$ 对奶牛彼此认识(是朋友)。第 $i$ 对彼此认识的奶牛通过两个不相同的整数 $A_i$ 和 $B_i$ 给定 $(1\le A_i \le N,\ 1 \le B_i \le N)$。
输入数据保证一对奶牛不会出现多次。 在喝茶时间活动中,如果奶牛 $i$ 和奶牛 $j$ 有一个相同的朋友奶牛 $k$,那么他们会在某次的喝茶活动中去认识对方(成为朋友),从而扩大他们的社交圈。
请判断,在喝茶活动举办很久以后(直到没有新的奶牛彼此认识),$Q\ (1 \le Q \le 100)$ 对奶牛是否已经彼此认识。询问 $j$ 包含一对不同的奶牛编号 $X_j,\ Y_j\ (1 \le X_j \le N,\ 1 \le Y_j \le N)$。
例如,假设共有 $1\ ..\ 5$ 头奶牛,我们知道 $2$ 号认识 $5$ 号,$2$ 号认识 $3$ 号,而且 $4$ 号认识 $5$ 号;如下图 (a)。
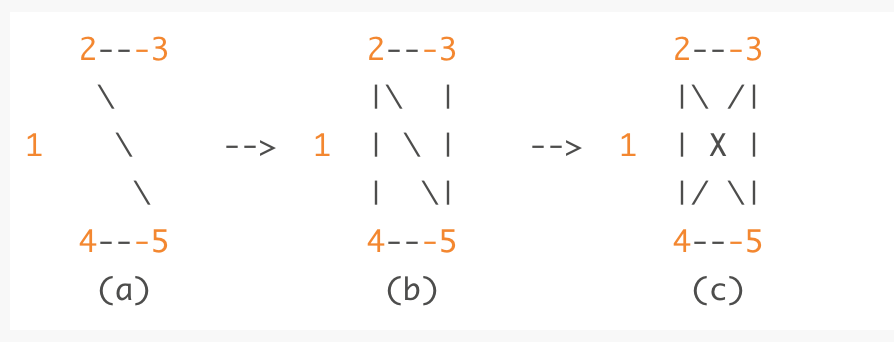
在某次的喝茶活动中,$2$ 号认识 $4$ 号,$3$ 号认识 $5$ 号;如上图(b)所示。接下来的喝茶活动中,$3$ 号认识 $4$ 号,如上图(c)所示。
Input
行 $1$:三个空格隔开的整数:$N,\ M,\ Q$。
行 $2\ .. M+1$:第 $i+1$ 行包含两个空格隔开的整数 $A_i,\ B_i$。
行 $M+2\ ..\ M+Q+1$:第 $j+M+1$ 行包含两个空格隔开的整数 $X_j,\ Y_j$,表示询问 $j$。
行 $2\ .. M+1$:第 $i+1$ 行包含两个空格隔开的整数 $A_i,\ B_i$。
行 $M+2\ ..\ M+Q+1$:第 $j+M+1$ 行包含两个空格隔开的整数 $X_j,\ Y_j$,表示询问 $j$。
Output
行 $1\ ..\ Q$:如果第 $j$ 个询问的两头奶牛认识, 第 $j$ 行输出 "Y"。如果不认识,第 $j$ 行输出 "N"。
Sample 1 Input
5 3 3
2 5
2 3
4 5
2 3
3 5
1 5
Sample 1 Output
Y
Y
N