Problem3802--Building Forest

3802: Building Forest

[Creator : ]
Time Limit : 2.000 sec  Memory Limit : 256 MiB

SubmitSolved: 0Submit Num: 0StatisticsShowOff!

Description

time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

An oriented weighted forest is an acyclic weighted digraph in which from each vertex at most one edge goes.

The root of vertex v of an oriented weighted forest is a vertex from which no edge goes and which can be reached from vertex v moving along the edges of the weighted oriented forest. We denote the root of vertex v as root(v).

The depth of vertex v is the sum of weights of paths passing from the vertex v to its root. Let's denote the depth of the vertex v as depth(v).

Let's consider the process of constructing a weighted directed forest. Initially, the forest does not contain vertices. Vertices are added sequentially one by one. Overall, there are n performed operations of adding. The i-th (i>0) adding operation is described by a set of numbers (k,v1,x1,v2,x2,... ,vk,xk) and means that we should add vertex number i and k edges to the graph: an edge from vertex root(v1) to vertex i with weight depth(v1)+x1, an edge from vertex root(v2) to vertex i with weight depth(v2)+x2 and so on. If k=0, then only vertex i is added to the graph, there are no added edges.

Your task is like this: given the operations of adding vertices, calculate the sum of the weights of all edges of the forest, resulting after the application of all defined operations, modulo 1000000007 (109+7).

Input

The first line contains a single integer n (1≤n≤105) − the number of operations of adding a vertex.

Next n lines contain descriptions of the operations, the i-th line contains the description of the operation of adding the i-th vertex in the following format: the first number of a line is an integer k (0≤k≤i-1), then follow 2k space-separated integers: v1,x1,v2,x2,... ,vk,xk (1≤vj≤i-1,|xj|≤109).

The operations are given in the order, in which they should be applied to the graph. It is guaranteed that sum k of all operations does not exceed 105, also that applying operations of adding vertexes does not result in loops and multiple edges.

Output

Print a single number − the sum of weights of all edges of the resulting graph modulo 1000000007 (109+7).

Examples
Input
6
0
0
1 2 1
2 1 5 2 2
1 1 2
1 3 4
Output
30
Input
5
0
1 1 5
0
0
2 3 1 4 3
Output
9
Note

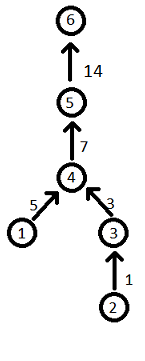
Conside the first sample:

  1. Vertex 1 is added. k=0, thus no edges are added.
  2. Vertex 2 is added. k=0, thus no edges are added.
  3. Vertex 3 is added. k=1. v1=2, x1=1. Edge from vertex root(2)=2 to vertex 3 with weight depth(2)+x1=0+1=1 is added.
  4. Vertex 4 is added. k=2. v1=1, x1=5. Edge from vertex root(1)=1 to vertex 4 with weight depth(1)+x1=0+5=5 is added. v2=2, x2=2. Edge from vertex root(2)=3 to vertex 4 with weight depth(2)+x1=1+2=3 is added.
  5. Vertex 5 is added. k=1. v1=1, x1=2. Edge from vertex root(1)=4 to vertex 5 with weight depth(1)+x1=5+2=7 is added.
  6. Vertex 6 is added. k=1. v1=3, x1=4. Edge from vertex root(3)=5 to vertex 6 with weight depth(3)+x1=10+4=14 is added.

The resulting graph is shown on the pictore below:

Source/Category

 
Submit