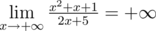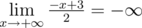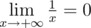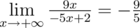Problem3796--Limit

3796: Limit

[Creator : ]
Time Limit : 2.000 sec  Memory Limit : 256 MiB

SubmitSolved: 0Submit Num: 0StatisticsShowOff!

Description

time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

You are given two polynomials:

  • P(x)=a0·xn+a1·xn-1+...+an-1·x+an and
  • Q(x)=b0·xm+b1·xm-1+...+bm-1·x+bm.

Calculate limit .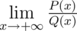

Input

The first line contains two space-separated integers n and m (0≤n,m≤100) − degrees of polynomials P(x) and Q(x) correspondingly.

The second line contains n+1 space-separated integers − the factors of polynomial P(x): a0, a1, ..., an-1, an (-100≤ai≤100,a0≠0).

The third line contains m+1 space-separated integers − the factors of polynomial Q(x): b0, b1, ..., bm-1, bm (-100≤bi≤100,b0≠0).

Output

If the limit equals +∞, print "Infinity" (without quotes). If the limit equals -∞, print "-Infinity" (without the quotes).

If the value of the limit equals zero, print "0/1" (without the quotes).

Otherwise, print an irreducible fraction − the value of limit 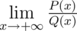, in the format "p/q" (without the quotes), where p is the − numerator, q (q>0) is the denominator of the fraction.

Examples
Input
2 1
1 1 1
2 5
Output
Infinity
Input
1 0
-1 3
2
Output
-Infinity
Input
0 1
1
1 0
Output
0/1
Input
2 2
2 1 6
4 5 -7
Output
1/2
Input
1 1
9 0
-5 2
Output
-9/5
Note

Let's consider all samples:

You can learn more about the definition and properties of limits if you follow the link: http://en.wikipedia.org/wiki/Limit_of_a_function

Source/Category

 
Submit