3743: Spider's Web
Description
Paw the Spider is making a web. Web-making is a real art, Paw has been learning to do it his whole life. Let's consider the structure of the web.
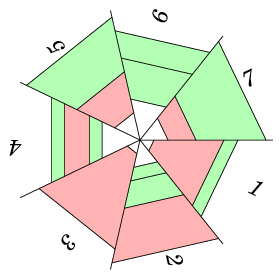
There are n main threads going from the center of the web. All main threads are located in one plane and divide it into n equal infinite sectors. The sectors are indexed from 1 to n in the clockwise direction. Sectors i and i+1 are adjacent for every i, 1≤i<n. In addition, sectors 1 and n are also adjacent.
Some sectors have bridge threads. Each bridge connects the two main threads that make up this sector. The points at which the bridge is attached to the main threads will be called attachment points. Both attachment points of a bridge are at the same distance from the center of the web. At each attachment point exactly one bridge is attached. The bridges are adjacent if they are in the same sector, and there are no other bridges between them.
A cell of the web is a trapezoid, which is located in one of the sectors and is bounded by two main threads and two adjacent bridges. You can see that the sides of the cell may have the attachment points of bridges from adjacent sectors. If the number of attachment points on one side of the cell is not equal to the number of attachment points on the other side, it creates an imbalance of pulling forces on this cell and this may eventually destroy the entire web. We'll call such a cell unstable. The perfect web does not contain unstable cells.
Unstable cells are marked red in the figure. Stable cells are marked green.
Paw the Spider isn't a skillful webmaker yet, he is only learning to make perfect webs. Help Paw to determine the number of unstable cells in the web he has just spun.
The first line contains integer n (3≤n≤1000) − the number of main threads.
The i-th of following n lines describe the bridges located in the i-th sector: first it contains integer ki (1≤ki≤105) equal to the number of bridges in the given sector. Then follow ki different integers pij (1≤pij≤105;1≤j≤ki). Number pij equals the distance from the attachment points of the j-th bridge of the i-th sector to the center of the web.
It is guaranteed that any two bridges between adjacent sectors are attached at a different distance from the center of the web. It is guaranteed that the total number of the bridges doesn't exceed 105.
Print a single integer − the number of unstable cells in Paw the Spider's web.
7
3 1 6 7
4 3 5 2 9
2 8 1
4 3 7 6 4
3 2 5 9
3 6 3 8
3 4 2 9
6