3598: Maxim and Increasing Subsequence
Description
Maxim loves sequences, especially those that strictly increase. He is wondering, what is the length of the longest increasing subsequence of the given sequence a?
Sequence a is given as follows:
- the length of the sequence equals n×t;
-
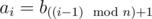(1≤i≤n×t), where operation 
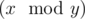means taking the remainder after dividing number x by number y.
Sequence s1,s2,...,sr of length r is a subsequence of sequence a1,a2,...,an, if there is such increasing sequence of indexes i1,i2,...,ir (1≤i1<i2<... <ir≤n), that aij=sj. In other words, the subsequence can be obtained from the sequence by crossing out some elements.
Sequence s1,s2,...,sr is increasing, if the following inequality holds: s1<s2<...<sr.
Maxim have k variants of the sequence a. Help Maxim to determine for each sequence the length of the longest increasing subsequence.
The first line contains four integers k, n, maxb and t (1≤k≤10;1≤n,maxb≤105;1≤t≤109;n×maxb≤2·107). Each of the next k lines contain n integers b1,b2,...,bn (1≤bi≤maxb).
Note that for each variant of the sequence a the values n, maxb and t coincide, the only arrays bs differ.
The numbers in the lines are separated by single spaces.
Print k integers − the answers for the variants of the sequence a. Print the answers in the order the variants follow in the input.
3 3 5 2
3 2 1
1 2 3
2 3 1
2
3
3