On Sum of Number of Inversions in Permutations - Problem

You are given a permutation p. Calculate the total number of inversions in all permutations that lexicographically do not exceed the given one.

As this number can be very large, print it modulo 1000000007 (10⁹+7).

Input

The first line contains a single integer n (1≤n≤10⁶) − the length of the permutation. The second line contains n distinct integers p₁,p₂,...,p_n (1≤p_i≤n).

Output

Print a single number − the answer to the problem modulo 1000000007 (10⁹+7).

Examples

Input

2
2 1

Output

Input

3
2 1 3

Output

Note

Permutation p of length n is the sequence that consists of n distinct integers, each of them is from 1 to n.

An inversion of permutation p₁,p₂,...,p_n is a pair of indexes (i,j), such that i<j and p_i>p_j.

Permutation a do not exceed permutation b lexicographically, if either a=b or there exists such number i, for which the following logical condition fulfills: 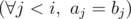$\text{[math]}$ AND (a_i<b_i).

3150: On Sum of Number of Inversions in Permutations

Description

Source/Category