2424: Acyclic Organic Compounds
Description
You are given a tree T with n vertices (numbered 1 through n) and a letter in each vertex. The tree is rooted at vertex 1.
Let's look at the subtree Tv of some vertex v. It is possible to read a string along each simple path starting at v and ending at some vertex in Tv (possibly v itself). Let's denote the number of distinct strings which can be read this way as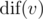 
.
Also, there's a number cv assigned to each vertex v. We are interested in vertices with the maximum value of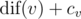 
.
You should compute two statistics: the maximum value of 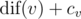and the number of vertices v with the maximum .
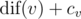The first line of the input contains one integer n (1≤n≤300000)− the number of vertices of the tree.
The second line contains n space-separated integers ci (0≤ci≤109).
The third line contains a string s consisting of n lowercase English letters− the i-th character of this string is the letter in vertex i.
The following n-1 lines describe the tree T. Each of them contains two space-separated integers u and v (1≤u,v≤n) indicating an edge between vertices u and v.
It's guaranteed that the input will describe a tree.
Print two lines.
On the first line, print 
over all 1≤i≤n.
On the second line, print the number of vertices v for which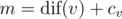 
.
10
1 2 7 20 20 30 40 50 50 50
cacabbcddd
1 2
6 8
7 2
6 2
5 4
5 9
3 10
2 5
2 3
51
3
6
0 2 4 1 1 1
raaaba
1 2
2 3
2 4
2 5
3 6
6
2
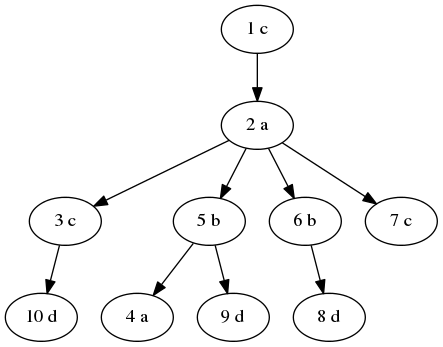
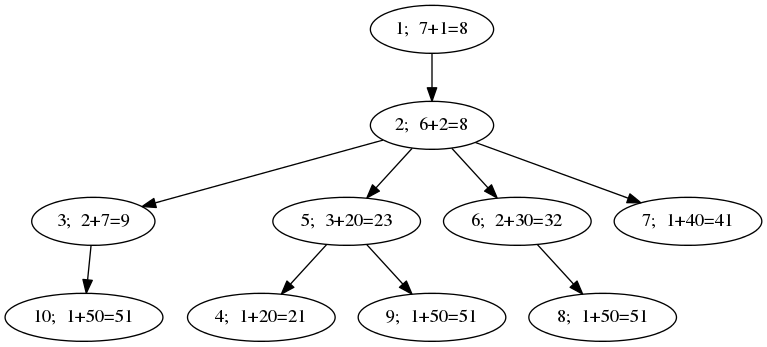
In the first sample, the tree looks like this:
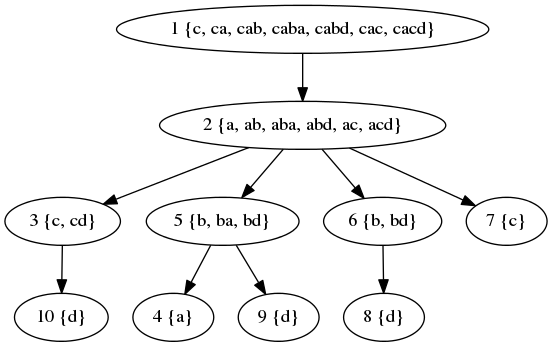
The sets of strings that can be read from individual vertices are:
Finally, the values of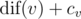 
are:
In the second sample, the values of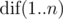 
are (5,4,2,1,1,1). The distinct strings read in T2 are 
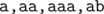; note that 
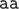can be read down to vertices 3 or 4.