Problem2407--Power Tree

2407: Power Tree

[Creator : ]
Time Limit : 2.000 sec  Memory Limit : 256 MiB

SubmitSolved: 0Submit Num: 0StatisticsShowOff!

Description

time limit per test
3.5 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Genos and Saitama went shopping for Christmas trees. However, a different type of tree caught their attention, the exalted Power Tree.

A Power Tree starts out as a single root vertex indexed 1. A Power Tree grows through a magical phenomenon known as an update. In an update, a single vertex is added to the tree as a child of some other vertex.

Every vertex in the tree (the root and all the added vertices) has some value vi associated with it. The power of a vertex is defined as the strength of the multiset composed of the value associated with this vertex (vi) and the powers of its direct children. The strength of a multiset is defined as the sum of all elements in the multiset multiplied by the number of elements in it. Or in other words for some multiset S:

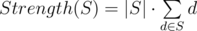
Saitama knows the updates that will be performed on the tree, so he decided to test Genos by asking him queries about the tree during its growth cycle.

An update is of the form 1pv, and adds a new vertex with value v as a child of vertex p.

A query is of the form 2u, and asks for the power of vertex u.

Please help Genos respond to these queries modulo 109+7.

Input

The first line of the input contains two space separated integers v1 and q (1≤v1<109, 1≤q≤200000) − the value of vertex 1 and the total number of updates and queries respectively.

The next q lines contain the updates and queries. Each of them has one of the following forms:

  • 1pivi, if these line describes an update. The index of the added vertex is equal to the smallest positive integer not yet used as an index in the tree. It is guaranteed that pi is some already existing vertex and 1≤vi<109.
  • 2ui, if these line describes a query. It is guaranteed ui will exist in the tree.

It is guaranteed that the input will contain at least one query.

Output

For each query, print out the power of the given vertex modulo 109+7.

Examples
Input
2 5
1 1 3
1 2 5
1 3 7
1 4 11
2 1
Output
344
Input
5 5
1 1 4
1 2 3
2 2
1 2 7
2 1
Output
14
94
Note

For the first sample case, after all the updates the graph will have vertices labelled in the following manner: 1 − 2 − 3 − 4 − 5

These vertices will have corresponding values: 2 − 3 − 5 − 7 − 11

And corresponding powers: 344 − 170 − 82 − 36 − 11

Source/Category

 
Submit