Problem2257--Bear and Colors

2257: Bear and Colors

[Creator : ]
Time Limit : 2.000 sec  Memory Limit : 256 MiB

SubmitSolved: 0Submit Num: 0StatisticsShowOff!

Description

time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

Bear Limak has n colored balls, arranged in one long row. Balls are numbered 1 through n, from left to right. There are n possible colors, also numbered 1 through n. The i-th ball has color ti.

For a fixed interval (set of consecutive elements) of balls we can define a dominant color. It's a color occurring the biggest number of times in the interval. In case of a tie between some colors, the one with the smallest number (index) is chosen as dominant.

There are 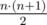non-empty intervals in total. For each color, your task is to count the number of intervals in which this color is dominant.

Input

The first line of the input contains a single integer n (1≤n≤5000)− the number of balls.

The second line contains n integers t1,t2,...,tn (1≤ti≤n) where ti is the color of the i-th ball.

Output

Print n integers. The i-th of them should be equal to the number of intervals where i is a dominant color.

Examples
Input
4
1 2 1 2
Output
7 3 0 0
Input
3
1 1 1
Output
6 0 0
Note

In the first sample, color 2 is dominant in three intervals:

  • An interval [2,2] contains one ball. This ball's color is 2 so it's clearly a dominant color.
  • An interval [4,4] contains one ball, with color 2 again.
  • An interval [2,4] contains two balls of color 2 and one ball of color 1.

There are 7 more intervals and color 1 is dominant in all of them.

Source/Category

 
Submit