Problem2056--Analysis of Pathes in Functional Graph

2056: Analysis of Pathes in Functional Graph

[Creator : ]
Time Limit : 2.000 sec  Memory Limit : 256 MiB

SubmitSolved: 0Submit Num: 0StatisticsShowOff!

Description

You are given afunctional graph. It is a directed graph, in which from each vertex goes exactly one arc. The vertices are numerated from $0$ to $n-1$.
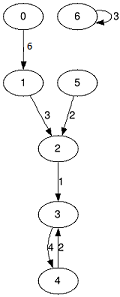
Graph is given as the array $f_0,f_1,...,f_{n-1}$, where $f_i$− the number of vertex to which goes the only arc from the vertex $i$. Besides you are given array with weights of the arcs $w_0,w_1,...,w_{n-1}$, where $w_i$− the arc weight from $i$ to $f_i$.
 
The graph from the first sample test. Also you are given the integer $k$ (the length of the path) and you need to find for each vertex two numbers $s_i$ and $m_i$, where:
  • $s_i$− the sum of the weights of all arcs of the path with length equals tokwhich starts from the vertex $i$;
  • $m_i$− the minimal weight from all arcs on the path with length $k$ which starts from the vertex $i$.
The length of the path is the number of arcs on this path.

Input

The first line contains two integers $n,k\ (1≤n≤10^5,1≤k≤10^{10})$. 
The second line contains the sequence $f_0,f_1,...,f_{n-1} (0≤f_i<n)$ and the third − the sequence $w_0,w_1,...,w_{n-1}\ (0≤w_i≤10^8)$.

Output

Print $n$ lines, the pair of integers $s_i, m_i$ in each line.

Sample 1 Input 

7 3
1 2 3 4 3 2 6
6 3 1 4 2 2 3

Sample 1 Output 

10 1
8 1
7 1
10 2
8 2
7 1
9 3

Sample 2 Input 

4 4
0 1 2 3
0 1 2 3

Sample 2 Output 

0 0
4 1
8 2
12 3

Sample 3 Input 

5 3
1 2 3 4 0
4 1 2 14 3

Sample 3 Output 

7 1
17 1
19 2
21 3
8 1

Source/Category

 
Submit