2019: CF711 - D. Directed Roads
Description
ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns $A_1,A_2,...,A_k\ (k>1)$ such that for every $1≤i<k$ there is a road from town $A_i$ to town $A_{i+1}$ and another road from town $A_k$ to town $A_1$. In other words, the roads are confusing if some of them form a directed cycle of some towns.
Now ZS the Coder wonders how many sets of roads (there are $2^n$ variants) in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.
Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.
Input
The first line of the input contains single integer $n\ (2≤n≤2·10^5)$ − the number of towns in Udayland.
The next line contains $n$ integers $a_1,a_2,...,a_n\ (1≤a_i≤n,\ a_i≠i)$, $a_i$ denotes a road going from town $i$ to town $a_i$.
Output
Sample 1 Input
3
2 3 1
Sample 1 Output
6
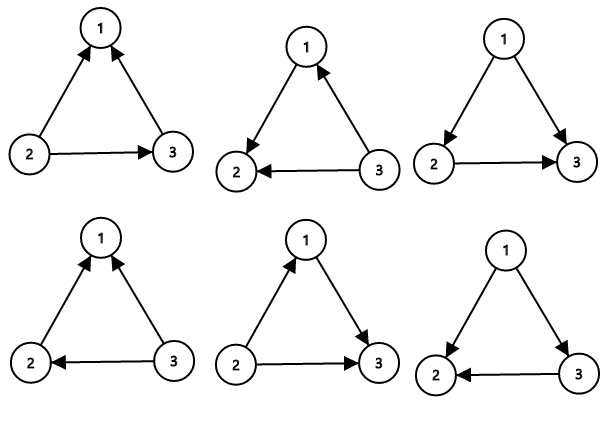
There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are $1 \to 3,2\to 3,3\to 1$ initially. Number the roads $1$ to $3$ in this order.
The sets of roads that ZS the Coder can flip (to make them not confusing) are {1},{2},{3},{1,2},{1,3},{2,3}. Note that the empty set is invalid because if no roads are flipped, then towns 1,2,3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.
The sample image shows all possible ways of orienting the roads from the first sample such that the network isnot confusing.
Sample 2 Input
4
2 1 1 1
Sample 2 Output
8
Sample 3 Input
5
2 4 2 5 3
Sample 3 Output
28