1670: Security System
Description
Fox Ciel safely returned to her castle, but there was something wrong with the security system of the castle: sensors attached in the castle were covering her.
Ciel is at point (1,1) of the castle now, and wants to move to point (n,n), which is the position of her room. By one step, Ciel can move from point (x,y) to either (x+1,y) (rightward) or (x,y+1) (upward).
In her castle, c2 sensors are set at points (a+i,b+j) (for every integer i and j such that: 0≤i<c,0≤j<c).
Each sensor has a count value and decreases its count value every time Ciel moves. Initially, the count value of each sensor is t. Every time Ciel moves to point (x,y), the count value of a sensor at point (u,v) decreases by (|u-x|+|v-y|). When the count value of some sensor becomes strictly less than 0, the sensor will catch Ciel as a suspicious individual!
Determine whether Ciel can move from (1,1) to (n,n) without being caught by a sensor, and if it is possible, output her steps. Assume that Ciel can move to every point even if there is a censor on the point.
In the first line there are five integers n,t,a,b,c (2≤n≤2·105, 0≤t≤1014, 1≤a≤n-c+1, 1≤b≤n-c+1, 1≤c≤n).
Please do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin stream (also you may use the %I64d specificator).
If Ciel's objective is possible, output in first line 2n-2 characters that represent her feasible steps, where i-th character is R if i-th step is moving rightward, or U if moving upward. If there are several solution, output lexicographically first one. Character R is lexicographically earlier than the character U.
If her objective is impossible, output Impossible.
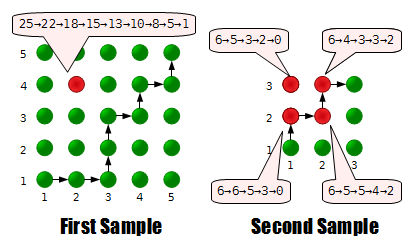
5 25 2 4 1
RRUURURU
3 6 1 2 2
URUR
3 5 1 2 2
Impossible
20 492 11 4 8
RRRRRRRRRRRRRRRRUUUUURUUUUURRUUUUUUUUU
The answers for the first sample and the second sample are shown on the picture: