1620: Vladik and Entertaining Flags
Description
In his spare time Vladik estimates beauty of the flags.
Every flag could be represented as the matrix n×m which consists of positive integers.
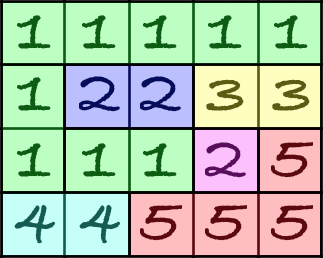
Let's define the beauty of the flag as number of components in its matrix. We call component a set of cells with same numbers and between any pair of cells from that set there exists a path through adjacent cells from same component. Here is the example of the partitioning some flag matrix into components:
But this time he decided to change something in the process. Now he wants to estimate not the entire flag, but some segment. Segment of flag can be described as a submatrix of the flag matrix with opposite corners at (1,l) and (n,r), where conditions 1≤l≤r≤m are satisfied.
Help Vladik to calculate the beauty for some segments of the given flag.
First line contains three space-separated integers n, m, q (1≤n≤10, 1≤m,q≤105)− dimensions of flag matrix and number of segments respectively.
Each of next n lines contains m space-separated integers− description of flag matrix. All elements of flag matrix is positive integers not exceeding 106.
Each of next q lines contains two space-separated integers l, r (1≤l≤r≤m)− borders of segment which beauty Vladik wants to know.
For each segment print the result on the corresponding line.
4 5 4
1 1 1 1 1
1 2 2 3 3
1 1 1 2 5
4 4 5 5 5
1 5
2 5
1 2
4 5
6
7
3
4
Partitioning on components for every segment from first test case: