1551: CF830 - D. Singer House
[Creator : ]
Description
It is known that passages in Singer house are complex and intertwined. Let's define a Singerk-house as a graph built by the following process:
take complete binary tree of heightkand add edges from each vertex to all its successors, if they are not yet present.
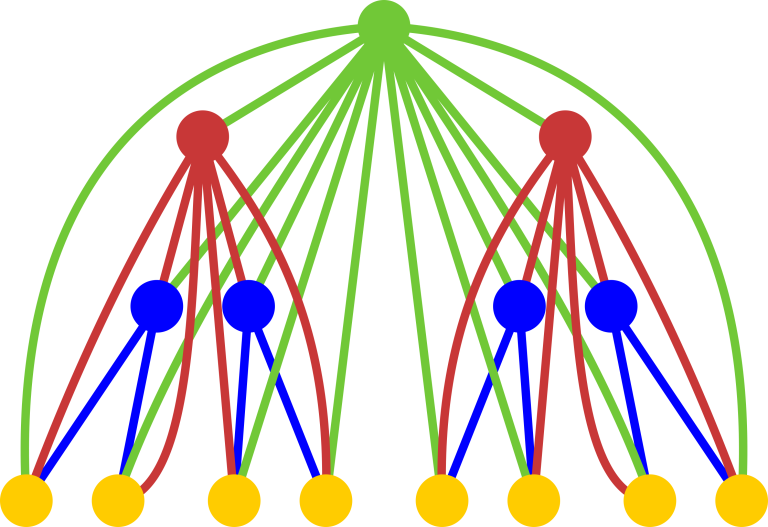
Singer4-house
Count the number of non-empty paths in Singerk-house which do not pass the same vertex twice. Two paths are distinct if the sets or the orders of visited vertices are different. Since the answer can be large, output it modulo $10^9+7$.
take complete binary tree of heightkand add edges from each vertex to all its successors, if they are not yet present.

Singer4-house
Count the number of non-empty paths in Singerk-house which do not pass the same vertex twice. Two paths are distinct if the sets or the orders of visited vertices are different. Since the answer can be large, output it modulo $10^9+7$.
Input
The only line contains single integer $k\ (1≤k≤400)$.
Output
Print single integer− the answer for the task modulo $10^9+7$.
Sample 1 Input
2
Sample 1 Output
9
There are 9 paths in the first example (the vertices are numbered on the picture below): 1, 2, 3, 1-2, 2-1, 1-3, 3-1, 2-1-3, 3-1-2.

Singer 2-house

Singer 2-house
Sample 2 Input
3
Sample 2 Output
245
Sample 3 Input
20
Sample 3 Output
550384565