1246: LOJ509 -「LibreOJ NOI Round #1」动态几何问题
[Creator : ]
Description
一天,神犇醒来时发现他的面前摆着一张初中数学试卷 …… 上面是这样一道题:
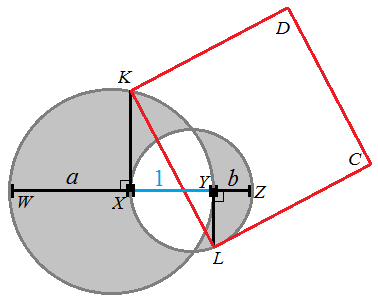
如图,已知两圆相交,作过两圆圆心的直线与两圆依次交于点 $W,\ X,\ Y,\ Z$,过 $X$ 作直线 $XK$ 垂直于 $WZ$ 交圆 WKY 于点 $K$,过 $Y$ 作直线 YL 垂直于 WZ 交圆 XLZ 于点 $L$,且 $K$ 和 $L$ 在直线的异侧。以 KL 为一边作正方形 KLCD。
(1). 已知 $XY=1,\ S_{KLCD}$ 为整数;设 $WX=a,\ YZ=b$,若 $a,\ b$ 都是整数且 $a\in [1,\ N],\ b\in [1,\ M]$,则有序数对 $(a,\ b)$ 共有多少种可能的取值?
神犇自然是秒了这道题。然而他发现不远处有一名抓耳挠腮丝毫不会的学生,看了十几分钟后神犇终于忍不住了,站起来大喊: 
(1). 已知 $XY=1,\ S_{KLCD}$ 为整数;设 $WX=a,\ YZ=b$,若 $a,\ b$ 都是整数且 $a\in [1,\ N],\ b\in [1,\ M]$,则有序数对 $(a,\ b)$ 共有多少种可能的取值?
你怎么这么菜啊?我来告诉你:由圆的性质显然可得 $KX=\sqrt a,\ YL=\sqrt b,\ ……$
但话还没说完,他就被监考老师拦住了,飒然惊觉的神犇才发现这是一场梦,只留下梦中的你在一脸苦闷地做着题。 Input
一行两个正整数 $N,\ M$。
Output
一行一个正整数,表示满足要求的有序整数对 $(a,\ b)$ 的种数。
Constraints
对于 $100\%$ 的数据,$1 \le N,\ M \le 1.5*10^{16}$。
$S_{KLCD}$ 表示正方形 KLCD 的面积。
$S_{KLCD}$ 表示正方形 KLCD 的面积。
| Subtask # | 分值 | $N$ | $M$ |
|---|---|---|---|
| 1 | $3$ | $\le 1$ | $\le 10^{15}$ |
| 2 | $5$ | $\le 5,000$ | $\le 5,000$ |
| 3 | $7$ | $\le 10^5$ | $\le 10^5$ |
| 4 | $3$ | $\le 10^6$ | $\le 10^6$ |
| 5 | $12$ | $\le 10^7$ | $\le 10^9$ |
| 6 | $9$ | $\le 10^9$ | $\le 10^9$ |
| 7 | $11$ | $\le 10^{11}$ | $\le 10^{11}$ |
| 8 | $10$ | $\le 10^{13}$ | $\le 10^{13}$ |
| 9 | $10$ | $\le 10^{15}$ | $\le 10^{15}$ |
| 10 | $8$ | $\le 10^{13}$ | $\le 5 \times 10^{15}$ |
| 11 | $17$ | $\le 3\times 10^{15}$ | $\le 3\times 10^{15}$ |
| 12 | $5$ | $\le 1.5\times 10^{16}$ | $\le 1.5\times 10^{16}$ |
Sample 1 Input
2 2
Sample 1 Output
2
Sample 2 Input
77777 66666
Sample 2 Output
495197
Sample 3 Input
1000000000 1000000000
Sample 3 Output
12735999860