爱丽丝的游戏由一个 $N\times M$ 的网格组成，网格中的每个格子都是以下三种类型中的一种。

1. 输送板：当玩家在上面时，它会将玩家向一个预先设定的方向移动。U,D,L,R 分别代表可以将玩家向上、下、左、右四个方向移动的输送板。

2. 石头地板：当玩家在上面时候，它会让玩家停下来。由 . 表示。

3. 冰地板：当玩家被移动到冰地板时，冰地板将延续玩家的移动状态，并继续按原移动方向移动玩家。由 # 表示。

需要特别注意，网格的最外圈总是由石头地板组成的。

一个有效网格的例子如下：

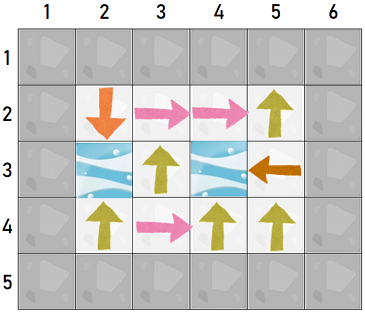
玩家只能从输送板开始。在那之后，玩家要么永远停留在移动状态中，要么以停在一个石头地板上结束。下面的情景是玩家从不同的输送板格开始的例子。

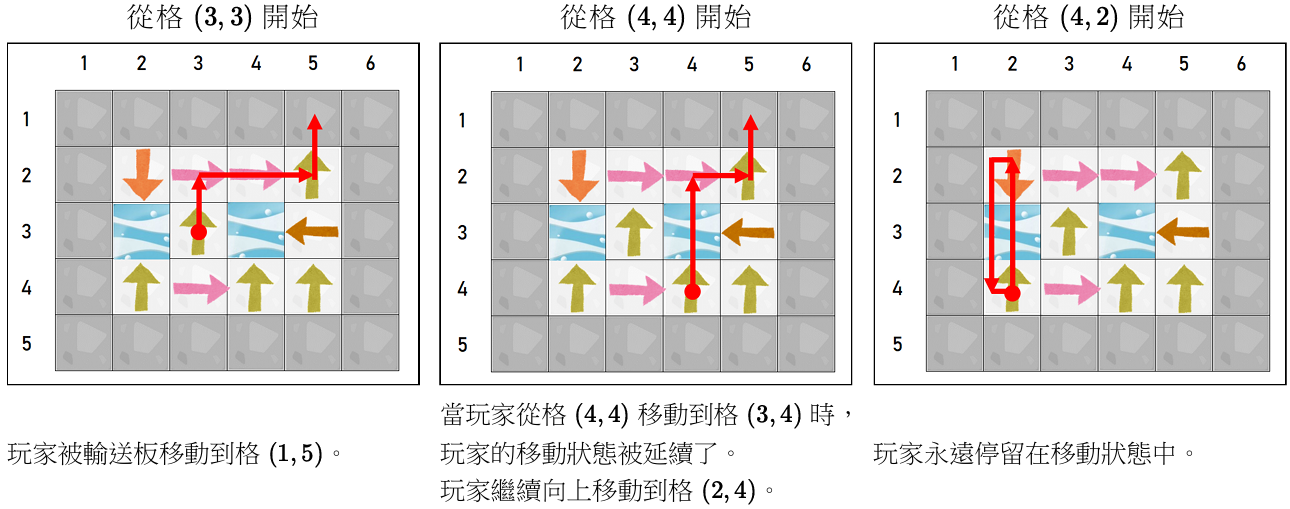
考虑玩家的所有起始位置，你能找到可能的结束位置的数量吗？

第一行输入两个整数 $N,M$，表示网格的行数和列数。

接下来的 $N$ 行，每行由 $M$ 个字符组成。

第 $i^{th}$ 行的 $j^{th}$ 个字符 $C_{i,j}$ 代表格 $(i,j)$ 的类型。

输出一个整数，表示可能的结束位置的数量。

$3 \leq N,M \leq 2,000$
$C_{i,j}$ 是 U,D,L,R,.,# 中的一个。
对于所有 $1\leq i\leq M,\ C_{1,i}=C_{N,i}=$.。
对于所有 $1\leq i\leq N,\ C_{i,1}=C_{i,M}=$.。

1

$(1,5)$ 是唯一可能的结束位置。

3

$(1,2),\ (1,6),\ (3,3)$ 是可能的结束位置。

1

$(2,9)$ 是唯一可能的结束位置。

4

$(1,2),\ (2,3),\ (3,4),\ (4,3)$ 是可能的结束位置。