It's that time of year again! The Annual Ruckus World Championships is fast approaching and you are absolutely determined to see Australia victorious. As the name implies, the goal of the competition is to be as loud and obnoxious as possible. Players compete in teams of at least $M$ people (there is no upper limit on team sizes). To make sure teams don't mix, team members must hold hands with each other.
Of course, youve found that there is nothing more obnoxious than spoilt kindergarteners, so youve rounded up $N$ of the loudest ones you could nd. You were hoping to send as many teams as possible, but some of the children have already started holding hands with their friends. Being as stubborn as they are, you are nding it rather di cult to convince them to let go of each other, or even to hold hands with anyone else.
Now for any other person, the story would end here; youd have to send whatever teams their friendships have forged. However, being the social engineering master you are, you have brought $K$  lollipops to use to bribe the children. You can pass a lollipop to the hand of a child, which will make them let go of the hand they are holding.
Using your $K$ lollipops, what is the largest number of teams with at least $M$ children you can form?

The first line of the input le will contain four space separated integers on a single line, in the format: $N$ $L$ $K$ $M$.

• $N$ is the number of children you have gathered.
• $L$ is the number of pairs of hands that are already joined together.
• $K$ is the number of lollipops you have.
• $M$ is the minimum size of a team. All teams must have at least $M$ people.

The following $L$ lines will each contain two integers, in the format: $l_i\ r_i$. This indicates that the $l_i$-th childs left hand is holding the $r_i$-th childs right hand. The children are numbered from $1$ to $N$. No one can hold their own hands.

Output should consist of a single integer: the maximum number of teams with at least $M$ children you can form.

3

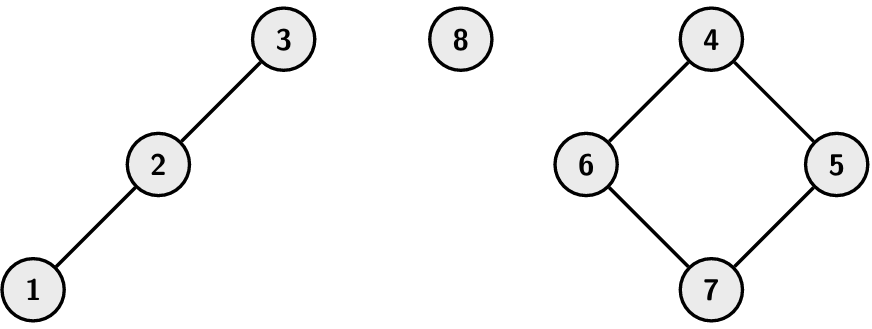
In the first example, you cannot break up any pair of hands (since you have no lollipops), and teams can have any number of people in them. Initially, the children have formed three teams: one of size 3, one of size 4 and one of size 1. Thus the output should be 3.

6

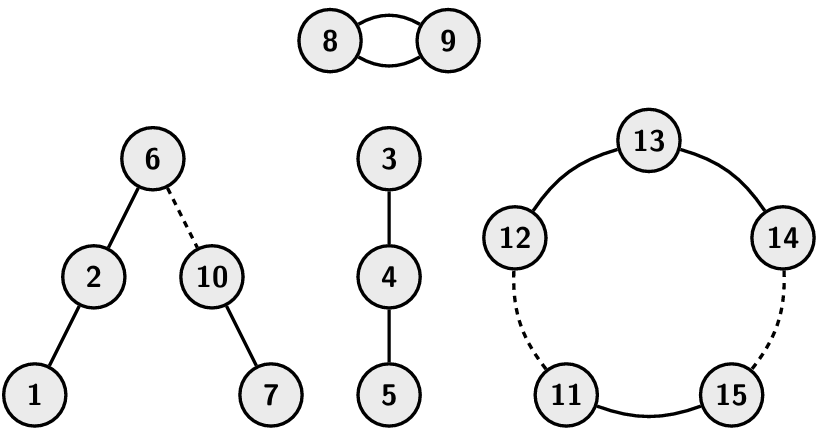
each team needs at least 2 people. Currently there are four teams of size 2,3,5 and 5. (The team of size 2 consists of children 8 and 9 holding both hands with each other.) By breaking the friendships 6 - 10,14 - 15,11 - 12, we can create up to six teams, of size 2,2,2,3,3 and 3. Thus the best answer is 6.
Note that even though we have 5 lollipops, we don't have to use them all in order to make the maximum number of teams (even though we can).