Have you ever heard of Melodramia, my friend? It is a land of magic forests and mysterious swamps, of sprinting heroines and dashing heroes. And it is home to two dragons, Rose and Scarlet, who, despite their competitive streak, are the best of friends.

• Rose and Scarlet love playing snap tag, a game for two players on an $R\times C$ grid. The game goes as follows:
• The two dragons start on different squares.
• Its Rose's turn first. On her turn she must move to an adjacent square (i.e. she must make one step left, right, up, or down).
• Its Scarlet's turn next. On her turn she must move to an adjacent square.
• The two dragons continue alternating turns...
• ...until one dragon lands on the same square as another. When this happens, the dragon who moved last shouts Snap tag! and wins the game.

Rose and Scarlet are both snap tag experts and always nd a winning strategy if one exists. If it is not possible for either player to gain the upper hand, then the game goes on forever.
In this task, you are given the size of the grid and the starting locations of both dragons. You must write a program to determine how the game ends: Does Rose win? Does Scarlet win? Does the game go on forever?

The input le will contain six space separated integers on a single line, in the format:
$R$ $C$ $r_{\text{ROSE}}$ $c_{\text{ROSE}}$ $r_{\text{SCARLET}}$ $c_{\text{SCARLET}}$.
$R$ and $C$ are the number of rows and columns in the grid, respectively.
$r_{\text{ROSE}}$ and $c_{\text{ROSE}}$ are the row and column of Roses starting square. (Rows are numbered $1$  to $R$ from top to bottom; columns are numbered $1$ to $C$ from left to right.)
$r_{\text{SCARLET}}$ and $c_{\text{SCARLET}}$ are the row and column of Scarlets starting square.

Output should consist of a single upper-case word with no punctuation.
If Rose can guarantee herself a win, output ROSE
If Scarlet can guarantee herself a win, output SCARLET
If neither player can guarantee a win, output DRAW

$1 \leq R,C \leq 10^9$

ROSE

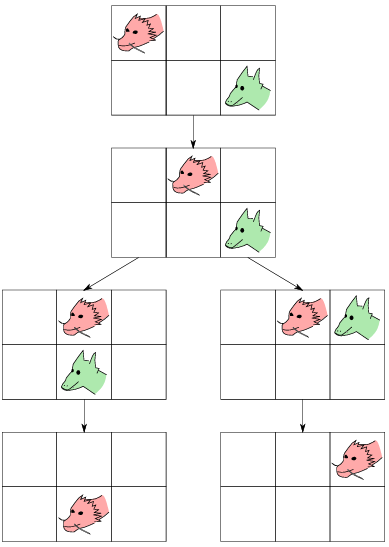
Rose can guarantee herself a win if she is clever and cautious.
On her first move, Rose steps to the right. Then, no matter whether Scarlet goes up or left on her turn, Rose can tag her the next turn.

SCARLET

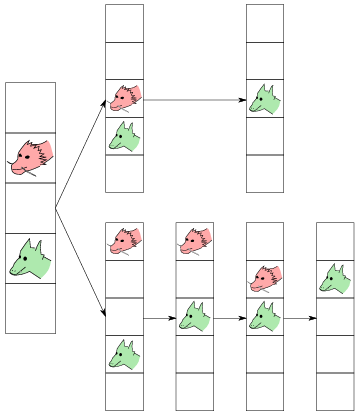
Scarlet can guarantee herself a win if she is clever and cautious.
If Rose moves down, then Scarlet will tag her on her very next turn. Otherwise, if Rose moves up, then Scarlet moves up and Rose will be forced to move down next to Scarlet, who will tag her the next turn.

ROSE

Rose can guarantee herself a win if she is clever and cautious.