Description

【分块】

分块（Sqrt Decomposition）是一种基于根号的算法，核心为大块标记，散块暴力，做到复杂度的平衡。
分块是一种思想，把一个整体划分为若干个小块，对整块整体处理，零散块单独处理。
块：我们将数列划分成若干个不相交的区间，每个区间称为一个块整块
整块：在一个区间操作时，完整包含于区间的块不完整的块
零散块：在一个区间操作时，只有部分包含于区间的块，即区间左右端点所在的两个块

分块对于其他数据结构的优点就是均分时间复杂度，还可以处理一些其他数据结构做不到的操作，分块本质上可以分为两种：

预处理答案，时间复杂度 $O(n\sqrt n+q)$。
在线处理答案，时间复杂度 $O(q\sqrt n+n)$。

当 $n,q$ 同值域时，这个显然没什么用，但是当 $q=nlog^2n$ 时，这个就显大作用了。
块状数组是把原序列划分成 $B$ 块，每块大小 $⌊\frac{n}{B}⌋$，我们询问对区间的整块整体处理，单独处理零散块，时间复杂度 $((B+⌊\frac{n}{B}⌋)$，其中 $B$ 取 $\sqrt n$ 时间复杂度最优。
分块实质上就是三层的树，每个非叶子结点的节点有 $\sqrt n$ 个子节点。

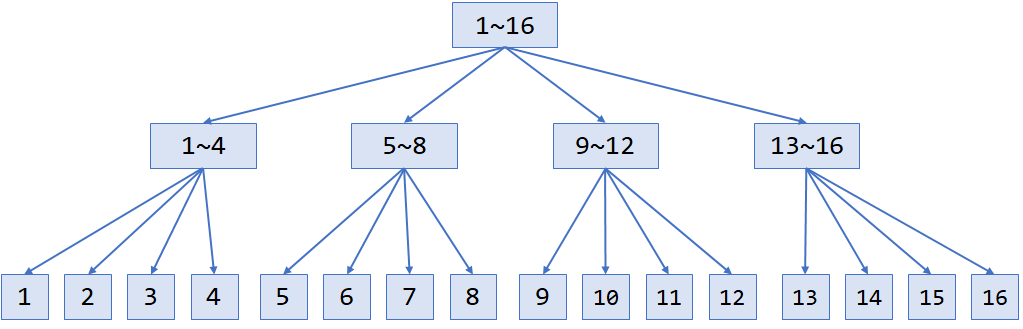
块状数组并不要求所维护信息满足结合律，也不需要一层层地传递标记，它具有更高的灵活性。

【问题引入】

给定一个长的为 $n$ 数列，求出任意区间 $[l,r]$ 的最大值 $(1\leq l\leq r\leq n)$。
当然我们可以使用线段树，树状数组来实现。但是分块怎么做呢？

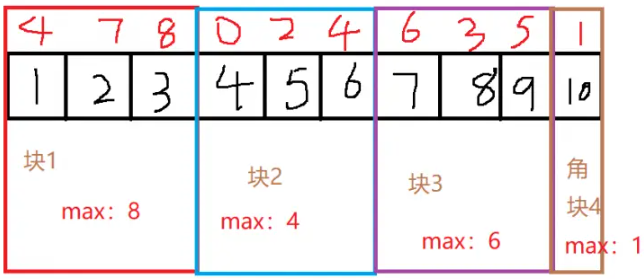
如图所示，我们的数据为 $4,7,8,0,2,4,6,3,5,1$，我们使用 $\sqrt 10=4$ 块，每块维护一下块内最大值。

当我们查询任意一个区间 $[l,r]$ 时，

$l$ 在的块与 $r$ 所在的块相同，如 $[1,2]$，则直接暴力查询即可，时间复杂度 $O(\sqrt n)$；
$l$ 在的块与 $r$ 不在一个块但是块是相邻的，一样是暴力查询，时间复杂度 $O(\sqrt n)$
若其块不相邻，如 $[1,10]$，我们先处理两边的边块角块，先暴力查询 $1$ 和 $10$ 所在的块内最大值，最后直接查询中间块内最大值即可，时间复杂度 $O(\sqrt n)$

所以总时间复杂度 $O(\sqrt n)$。

Input

【问题一：只查询】

【预处理】

我们根据定义可以写出如下代码：

void init(int n){
    bl=sqrt(n);//每一块大小
    for(ll i=1;i<=bl;i++){
        L[i]=(i-1)*bl+1;//第i个块的左端点
        R[i]=i*bl;//第i个块的右端点
    }
    if(R[bl]<n) {
        bl++;
        L[bl]=R[bl-1]+1;
        R[bl]=n;
    }
    //标记每个数它所属的块编号
    for(int i=1;i<=bl;i++){
        for(int j=L[i];j<=R[i];j++){
            pos[j]=i;
        }
    }
    //预处理每个块的大小
    for (int i=1;i<=bl;i++){
        sz[i]=R[i]-L[i]+1;
    }
}

其中 bl 表示块的数量，L 表示第 $i$ 个块的左端点，$R$ 表示右端点，还要判断最后是否还有块。

当然，为了方便计算，我们标记每个数它所属的块编号，预处理每个块的大小。

【区间查询】

这里我们查询 $[x,y]$ 的最大值。
预处理每块的最大值。mx[i] 表示第 $i$ 块的最大值。

//处理每块的最大值 
for(int i=1;i<=bl;i++){
    mx[i]=-INF;
    for(int j=st[i];j<=ed[i];j++){
        mx[i]=max(mx[i],a[j]);
    }
}

如果左右两边在同一块，直接暴力查询区间。

否则，暴力计算零碎块，再查找连续块。

int ql=pos[l];//查询块起点 
int qr=pos[r];//查询块终点
int ans=-INF;
if(ql==qr){
    //同一块
    for(int i=l;i<=r;i++){
        ans=max(ans,a[i]);
    } 
}else{
    //查询最左边块 
    for(int i=l;i<=ed[ql];i++){
        ans=max(ans,a[i]);
    }
    //查询最右边块 
    for(int i=st[qr];i<=r;i++){
        ans=max(ans,a[i]);
    }
    //查询中间连续块 
    for(int i=ql+1;i<qr;i++) {
        ans=max(ans,mx[i]);
    }
}