【问题 1: Static Count of Lesser Elements range queries.】

The problem statement is: Given an input array $a_1,a_2,\cdots,a_n$ of size $n$ and $q$ queries. Every query has three arguments, $l, r,k$. We need to print the $k$-th smallest element in the range from $l$ to $r$. $l$ and $r$ mark the start and end of the subarray, respectively.

A[] = {3, 4, 0, 6, 8, 1} 
Q = [4, 5, 2] 
Answer: 8
The 2nd smallest element in the subarray {8, 1} is 8.

【Naive Approach】

For any query(l, r, k), we first create a temporary array ‘temp’. We copy the elements of the array from $i = l$ to $r$ into temp. Then we sort temp. Finally, we print temp[k - 1] as the answer. This approach is quite easy to implement. 

The time complexity of this approach is $O(NlogN)$ as we are sorting. The space complexity is $O(N)$ as we are using temp as an auxiliary array. 

【Efficient Approach】

The idea is to build a merge sort tree(segment tree) in which every node contains an array of sorted elements of the subarray that is represented by that node. For more clarity, refer to the image attached below. For querying, the same traditional methodology is followed. However, everything is discussed in the next section.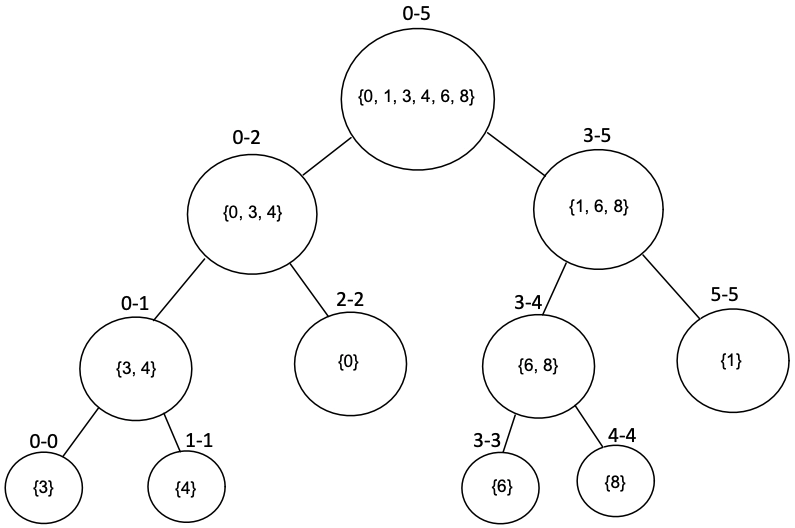

【Algorithm】

1. Declare a global 2D array ‘seg’, that refers to the merge sort tree. As already mentioned, every node contains a sorted subarray, ranging from ‘low’ to ‘high’.
2. Define a function buildST(idx, low, high, input), that builds the merge sort tree recursively:
2.1 Understanding the parameters: A node is defined on the range ‘low’ to ‘high’. The node's data is stored in seg[idx] or, essentially, the node = seg[idx]. ‘input’ is the input array.
2.2 Base case: when low = high, this means, that the range consists of only one element. Hence, simply set seg[i] = input[low]. 
2.3 Else, calculate mid = (low + high) / 2.
2.4 Recursively, call ‘buildST(2 * idx + 1, low, mid, input)’ and buildST(2 * idx + 2, mid + 1, high, input) to build the left and right subtrees. If the current node is seg[idx], the left node is seg[2 * idx + 1] and the right node is seg[2 * idx + 2]. This is an important property of merge sort trees.  
2.5 After recursively building the left and right subtrees, the values of left and right nodes are used to build the current node. FYI, the left and right node store sorted subarrays in a range [low, mid] and [mid + 1, high], which are merged to construct a new bigger subarray that is stored in seg[idx], i.e. the current node. 
3. Define a wrapper function ‘query(l, r, k, n)’ as: 
3.1 ‘l’ is the start, and ‘r’ is the end of the query range. ‘k’ denotes that the Kth smallest number in the given range has to be returned. ‘n’ is the total number of elements in the ‘input’ array. 
3.2 This function calls ‘queryHelper(idx, l, r, low, high)’, which does all the heavy lifting and returns a sorted subarray in the range [l, r]. ‘idx’ points to the node corresponding to the range [low, high], a query range is bounded by [l, r]. 
3.3 This function is defined as: 
3.3.1 When the node lies completely inside the range [l, r] return seg[idx].
3.3.2 When the node lies completely outside the range [l, r], return an empty array.
3.3.3 Else, recursively call for the left child i.e. queryHelper(2 * idx + 1, l, r, low, mid) and queryHelper(2 * idx + 2, l, r, mid + 1, high), store the answers in ‘left’ and ‘right’ arrays, respectively, merge them and return the merger array. 
3.4 The wrapper function makes a call to queryHelper(0, l, r, 0, n - 1), stores the answer of the call into an array and returns the element at the (k - 1)th index. 

【Code】

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,q,a[N];
vector<int> seg[4*N+5];
//build merge sort tree
void build(int node,int l,int r){
    //if range length is 1 there's only one element to add and no children
    if (l==r){
        seg[node].push_back(a[l]);
        return;
    }int mid=(l+r)/2;
    build(node*2,l,mid);
    build(node*2+1,mid+1,r);
    int i=0,j=0;
    // use two pointers to merge the two vectors in O(r-l+1)
    while (i<seg[node*2].size() && j<seg[node*2+1].size()){
        if (seg[node*2][i]<seg[node*2+1][j]) seg[node].push_back(seg[node*2][i++]);
        else seg[node].push_back(seg[node*2+1][j++]);
    }
    while (i<seg[node*2].size()) seg[node].push_back(seg[node*2][i++]);
    while (j<seg[node*2+1].size()) seg[node].push_back(seg[node*2+1][j++]);
    return;
}
//query
int query(int node,int l,int r,int lx,int rx,int x){
    //if outside -> 0
    if (l>rx || r<lx) return 0;
    //if inside do binary search
    if (l>=lx && r<=rx){
        int L=0,R=seg[node].size()-1,mid,ans=0;
        while (L<=R){
            mid=(L+R)/2;
            if (seg[node][mid]<x){
                ans=mid+1;
                L=mid+1;
            }else R=mid-1;
        }return ans;
    }
    int mid=(l+r)/2;
    return query(node*2,l,mid,lx,rx,x)+query(node*2+1,mid+1,r,lx,rx,x);
}
int main(){
    cin>>n>>q;
    for (int i=1;i<=n;i++) cin>>a[i];
    build(1,1,n);
    while (q--){
        int l,r,x;
        cin>>l>>r>>x;
        cout<<query(1,1,n,l,r,x)<<endl;
    }
    return 0;
}

【例题】

SPOJ MKTHNUM。
SPOJ GIVEAWAY。
SPOJ KQUERY。
CF216E Valera and Queries。

【Problem 2: Dynamic Lower Bound problem】

We are given an array $a_1,a_2,a_3...a_n$ and an integer $q$. The $i$_th of the next $q$ lines has an integer $t_i$, describing the type of query.

• If $t_i=0$ then you are given two other integers, $idx_i$ and $x_i$, meaning that we should make $a_{idx}=x_i$.

• If $t_i=1$ then you are given three integers $l_i,r_i,x_i$. You should answer with the smallest value $v$ in the range $[l_i,r_i]$ such that $x≤v$. If there is none, print $-1$.

【Solution】

Let's create something similar to merge sort tree, where each node has a multiset of the elements in its range, we can loop through these values. Building time complexity is $O(nlog^2n)$ because we add each element $logn$ times with time complexity $O(logn)$ because multiset. Now to the queries. When we are supposed to change some element, we go through the segment tree and remove it from each node that contains it and add its new value instead. This is also in $O(log^2n)$ because we add to $logn$ nodes at most, each with time complexity $O(logn)$ because multiset. Now for the other type of queries, we do similar to the previous problem. If a node is outside the query range we return INF. If a node is entirely inside the query range we return the lower bound in this node's multiset. Else we want the minimum of the answer of the node's right child and left child answers. Time complexity of this queries is $O(log^2n)$ because we go through $logn$ nodes at worst case each with time complexity $O(logn)$ because of binary search (lower bound function). Time compleixty overall: $O((q+n)log^2n)$.

【Code】

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,q,a[N];
multiset<int> seg[4*N+5];
void build(int node,int l,int r){
    if (l==r){
        seg[node].insert(a[l]);
        return;
    }int mid=(l+r)/2;
    build(node*2,l,mid);
    build(node*2+1,mid+1,r);
    for (int i=l;i<=r;i++) seg[node].insert(a[i]);
    return;
}
void edit(int node,int l,int r,int idx,int val){
    if (l==r){
        seg[node].erase(a[idx]);
        seg[node].insert(val);
        return;
    }int mid=(l+r)/2;
    if (idx<=mid) edit(node*2,l,mid,idx,val);
    else edit(node*2+1,mid+1,r,idx,val);
    seg[node].erase(a[idx]);
    seg[node].insert(val);
    return;
}
int query(int node,int l,int r,int lx,int rx,int x){
    if (l>rx || r<lx) return INT_MAX;
    if (l>=lx && r<=rx){
        auto it=seg[node].lower_bound(x);
        if (it==seg[node].end()) return INT_MAX;
        return *it;
    }int mid=(l+r)/2;
    return min(query(node*2,l,mid,lx,rx,x),query(node*2+1,mid+1,r,lx,rx,x));
}
int main(){
    ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
    cin>>n>>q;
    for (int i=1;i<=n;i++) cin>>a[i];
    build(1,1,n);
    while (q--){
        bool t;cin>>t;
        if (!t){
            int idx,val;
            cin>>idx>>val;
            edit(1,1,n,idx,val);
            a[idx]=val;
            continue;
        }int l,r,x;cin>>l>>r>>x;
        int y=query(1,1,n,l,r,x);
        if (y==INT_MAX) cout<<-1<<endl;
        else cout<<y<<endl;
    }
    return 0;
}