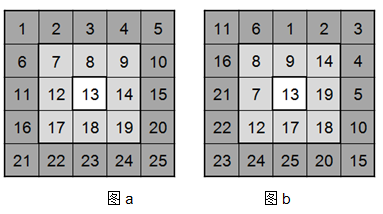
一个 $n×n\ (n\leq 6)$ 的矩阵，可以分成一些环。如图中，$n=5$，可以划分成 $3$ 个环。
每个环上的数字都可以沿着环顺时针或者逆时针转动，每次转动只能将任意一个环顺时针或者逆时针转动一格。
初始状态如图a，将矩阵从左到右、从上到下依次用 $1$ 到 $n×n$ 填满。
现在给你一个局面，请问至少通过多少次环的转动能使矩阵恢复到初始状态？

例如，图b的局面可以通过，最外圈逆时针转动两格，第二圈顺时针转动一格，恢复到初始状态（图a），即至少转动三次。

第一行输入一个正整数 $n$。

接下来 $n$ 行，每行输入 $n$ 个用空格隔开的正整数，第 $i$ 行第 $j$ 个数 $a_{ij}\ (a_{ij}≤1000)$，表示给定的 $n×n$ 的矩阵局面。

若给定的矩阵局面可以通过环的转动回到初始状态，则输出两行，第一行为 YES，第二行为一个非负整数，表示至少需要转动几次；否则，输出 NO。