【前置知识】

高维前缀和，状压DP。

【超集】

如果集合A是集合B的子集，那么B就是A的超集。

【问题】

我们考虑一个关于求和的问题，$\forall i$，求 $\sum_{j⊂i} a_j$，
这里 $j$ 属于 $i$ 的定义可以很宽泛，我们可以将其定义为 $j|i$，也可以是 $j$ 的二进制表示是 $i$ 的二进制表示的子集等等。
显然一种暴力的方法就是枚举 $i$ 的所有子集。
考虑优化的话，我们可以尝试前缀和，因为显然如果有 $j⊂z,z⊂i$，我们可以将 $j$ 的贡献都先算在 $z$ 上面再传给 $i$，而不必一个个来。

【二进制子集前缀和】

$\forall i,\ 0\leq i \leq 2^n-1$，求 $\sum_{j⊂i} a_j$，其中 $j$ 属于 $i$ 定义为 $j$ 的二进制表示是 $i$ 的二进制表示的子集。

for(int j=0;j<n;++j){
    for(int i=0;i<(1<<n);++i){
        if(i&(1<<j)){
            dp[i]+=dp[i^(1<<j)]
        }
    }
}

因为是正序枚举的，所以 i^(1<<j) 是是当前这一维度，而此时 $i$ 还在上一维，所以这样就实现了高维的前缀和。
这样的时间复杂度是 $O(n*2^n)$。而如果去枚举子集来做前缀和的话，时间复杂度是 $O(n^3)$ 的。

高维前缀和学习笔记-CSDN博客

Input

【SOS dp】

有时，我们会碰到一些问题：求一些数的所有集合之和。
$F[\text{mask}]=\sum_{i \in \text{mask}} A[i]$
我们说 $i \in \text{mask}$ 即为 i & mask = i。
下面来举个例子：
有 $n$ 个数，这些数分别是 $a_1 , a_2 , a_3 ...... a_n$。
假设 $n=5,\ a[5]=\{ 12 , 34 , 45 , 28 , 37\}$。
这些数的下标分别是 $1,2,3,4,5$。
这些数的下标可以形成的集合有：

{1}, {2}, {3}, {4}, {5},
{1,2}, {2,3}, {3,4}, {4,5},
{1,2,3}, {2,3,4}, {3,4,5},
{1,2,3,4}, {2,3,4,5},
{1,2,3,4,5}

设每个集合中的数的和为 $A_i$，$i$ 表示每个集合（用二进制数表示），
$f_{mask}$ 表示集合 mask 的子集之和。

【方法一：暴力枚举】

时间复杂度 $O(4^n)$。

for(int mask =0;mask < (1<<N); ++i){
    for(int i = 0;i < (1<<N); ++i){
        if(i&mask == i){
            F[mask] += A[i];
        }
    }
}

【方法二：暴力枚举】

时间复杂度通过二项式定理的 $O(3^n)$ 枚举所有子集。

for(int mask = 0;mask < (1<<N); ++mask){
    F[mask] = A[0];
    for(int i = mask; i > 0; i = (i-1)&mask){
        F[mask] += A[i];
    }
}

【方法三：SOS DP】

dp[mask][i] 代表 x & mask=x, x ^ mask < $2^{i+1}$ 的 A[x] 的和。意思就是 dp[mask][i] 是和 mask 只有前 $i$ 个位不同的 A[x] 的和。
dp[mask][i] = dp[mask][i-1]，如果 mask & ($2^i$)=0
dp[mask][i] = dp[mask][i-1]+dp[mask ^ ($2^i$)][i-1]，如果 mask & ($2^i$)=$2^i$。
如下图。

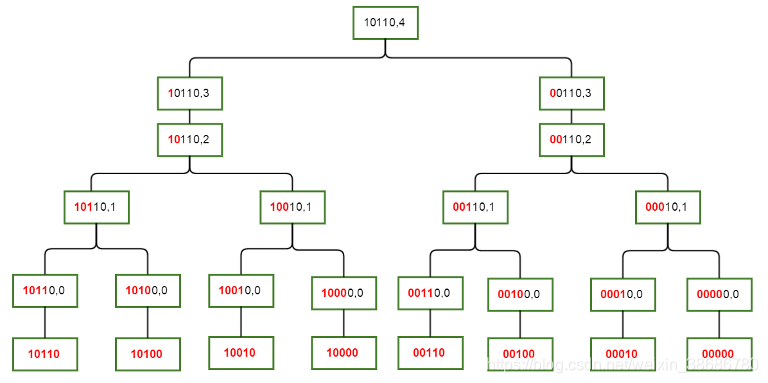
//iterative version
for(int mask = 0; mask < (1<<N); ++mask){
    dp[mask][-1] = A[mask];	//handle base case separately (leaf states)
    for(int i = 0;i < N; ++i){
        if(mask & (1<<i)){
            dp[mask][i] = dp[mask][i-1] + dp[mask^(1<<i)][i-1];
        }else{
            dp[mask][i] = dp[mask][i-1];
        }
    }
    F[mask] = dp[mask][N-1];
}

SOS DP_sosdp-CSDN博客
当然，有的时候二维数组是开不下的，我们就要优化空间。
我们发现，当前一层的运算只和他的上一层有关，我们可以考虑将二维转化为一维。
所以就变成了如下程序：

//memory optimized, super easy to code.
for(int i = 0; i<(1<<N); ++i){
    F[i] = A[i];
}
for(int i = 0;i < N; ++i) for(int mask = 0; mask < (1<<N); ++mask){
    if(mask & (1<<i)){
        F[mask] += F[mask^(1<<i)];
    }
}

这两个代码的时间复杂度为 $O(n\times 2^n)$。

Output

【例题】

https://blog.csdn.net/weixin_75161465/article/details/136768895

11362: 学习系列 —— SOS DP

Description