【一维前缀和】

for(int i=1;i<=n;++i){
    a[i]+=a[i-1];	
}

【二维前缀和】

这里我们一般用容斥来处理。

for(int i=1;i<=n;++i){
    for(int j=1;j<=m;++j){
        sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];	
    }	
} 

如果到了三维的话，也是可以容斥的，写起来就有点烦。我们还有另外一种写二维前缀和的方法。

for(int i=1;i<=n;++i){
    for(int j=1;j<=m;++j){
        sum[i][j]+=sum[i][j-1];
    }
}
for(int i=1;i<=n;++i){
    for(int j=1;j<=m;++j){
        sum[i][j]+=sum[i-1][j];	
    }
}

这个其实很好理解

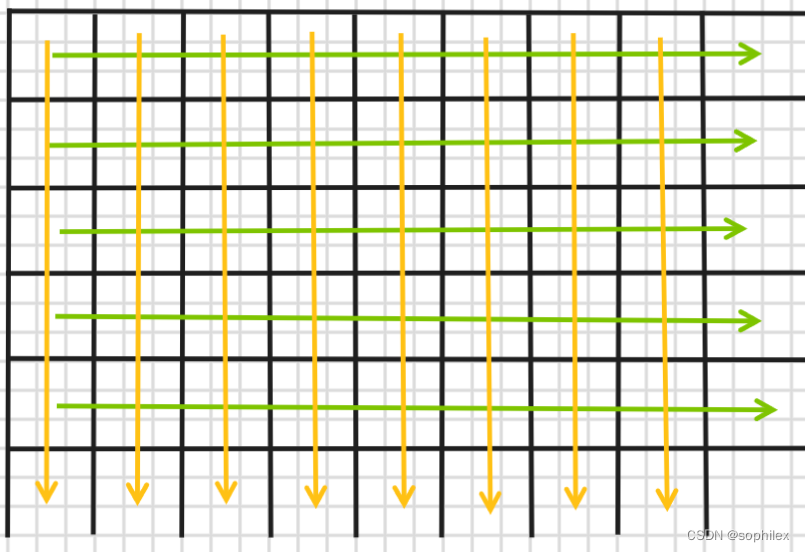
我们先按绿色方向把每一层的前缀和都给做出来，然后再沿黄色方向做一遍前缀和，按顺序从小往大走的话，显然我们会把第一维（行）的前缀和算进去。

【三维前缀和】

所以不难得到三维的前缀和。

for(int i=1;i<=n;++i){
    for(int j=1;j<=m;++j){
        for(int k=1;k<=q;++k){
            sum[i][j][k]+=sum[i-1][j][k];
        }
    }
}
for(int i=1;i<=n;++i){
    for(int j=1;j<=m;++j){
        for(int k=1;k<=q;++k){
            sum[i][j][k]+=sum[i][j-1][k];
        }
    }
}
for(int i=1;i<=n;++i){
    for(int j=1;j<=m;++j){
        for(int k=1;k<=q;++k){
            sum[i][j][k]+=sum[i][j][k-1];
        }
    }
}

【高维前缀和】

那么如果扩展到了n维会怎么样？
思路跟上面是一样的，就是一维一维的做前缀和。

for(int i[1]=1;i[1]<=n;i[1]++)
    for(int i[2]=1;i[2]<=n;i[2]++)
        //...
        a[i[1]][i[2]][i[3]]...+=a[i[1]-1]...;
...

【三维前缀和】

求 (0,0,0) 到 (x,y,z) 的三维前缀和。
直接计算公式

S(X, Y, Z) = a(X, Y, Z)
+S(X, Y, Z - 1) + S(X, Y - 1, Z) + S(X - 1, Y, Z)
-S(X, Y - 1, Z - 1) - S(X - 1, Y, Z - 1) - S(X - 1, Y - 1, Z)
+S(X - 1, Y - 1, Z - 1)

便于记忆的方法：二进制 001——111，奇数个（-1）则为正号。

S(x,y,z)=a(x,y,z)+	表示
001 符号 +	S(x,y,z-1)
010 符号 +	S(x,y-1,z)
011 符号 -	S(x,y-1,z-1)
100 符号 +	S(x-1,y,z)
101 符号 -	S(x-1,y,z-1)
110 符号 -	S(x-1,y-1,z)
111 符号 +	S(x-1,y-1,z-1)

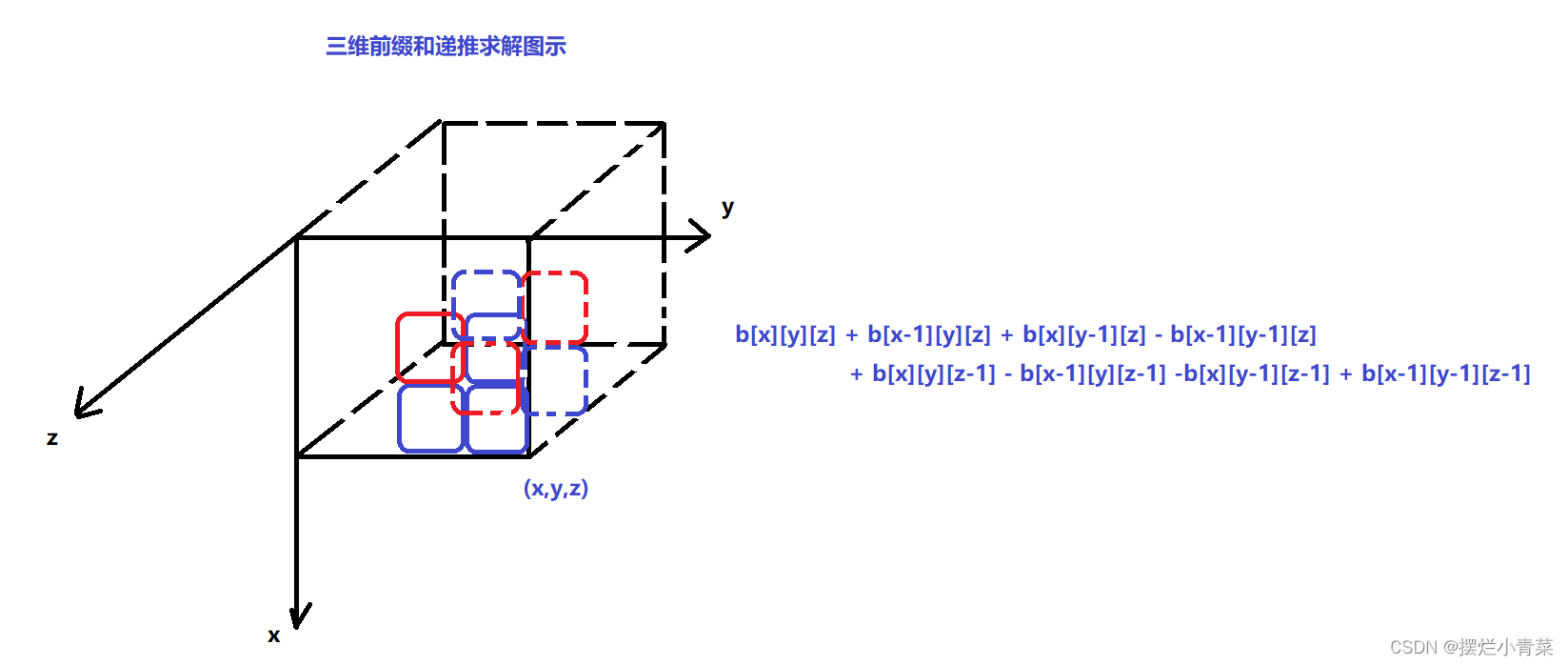
【三维差分】

求 (x1,y1,z1) 到 (x2,y2,z2) 的差分。

二进制	表示
000 符号 +	B(x1,y1,z1)+=c
001 符号 -	B(x1,y1,z2+1)-=c
010 符号 -	B(x1,y2+1,z1)-=c
011 符号 +	B(x1,y2+1,z2+1)+=c
100 符号 -	B(x2+1,y1,z1)-=c
101 符号 +	B(x2+1,y1,z2+1)+=c
110 符号 +	B(x2+1,y2+1,z1)+=c
111 符号 -	B(x2+1,y2+1,z2+1)-=c