11353: 洛谷P4467 - [SCOI2007] k短路
[Creator : ]
Description
有 $n$ 个城市和 $m$ 条单向道路,城市编号为 $1$ 到 $n$。每条道路连接两个不同的城市,且任意两条道路要么起点不同要么终点不同,因此 $n$ 和 $m$ 满足$m \le n(n-1)$。
给定两个城市 $a$ 和 $b$,可以给 $a$ 到 $b$ 的所有简单路(所有城市最多经过一次,包括起点和终点)排序:先按长度从小到大排序,长度相同时按照字典序从小到大排序。你的任务是求出 $a$ 到 $b$ 的第 $k$ 短路。
给定两个城市 $a$ 和 $b$,可以给 $a$ 到 $b$ 的所有简单路(所有城市最多经过一次,包括起点和终点)排序:先按长度从小到大排序,长度相同时按照字典序从小到大排序。你的任务是求出 $a$ 到 $b$ 的第 $k$ 短路。
Input
输入第一行包含五个正整数 $n,m,k,a,b$。
以下 $m$ 行每行三个整数 $u,v,l$,表示从城市 $u$ 到城市 $v$ 有一条长度为 $l$ 的单向道路。
以下 $m$ 行每行三个整数 $u,v,l$,表示从城市 $u$ 到城市 $v$ 有一条长度为 $l$ 的单向道路。
Output
如果 $a$ 到 $b$ 的简单路不足 $k$ 条,输出 `No`,否则输出第 $k$ 短路:从城市 $a$ 开始依次输出每个到达的城市,直到城市 $b$,中间用减号 `-` 分割。
Constraints
- $20\%$ 的数据满足:$n\leq 5$;
- $40\%$ 的数据满足:$n\leq 30$;
- $100\%$ 的数据满足:$2\leq n\leq 50$,$1\leq k\leq 200$,$1\le l\le 10^4$。
- $40\%$ 的数据满足:$n\leq 30$;
- $100\%$ 的数据满足:$2\leq n\leq 50$,$1\leq k\leq 200$,$1\le l\le 10^4$。
Sample 1 Input
5 20 10 1 5
1 2 1
1 3 2
1 4 1
1 5 3
2 1 1
2 3 1
2 4 2
2 5 2
3 1 1
3 2 2
3 4 1
3 5 1
4 1 1
4 2 1
4 3 1
4 5 2
5 1 1
5 2 1
5 3 1
5 4 1
Sample 1 Output
1-2-4-3-5
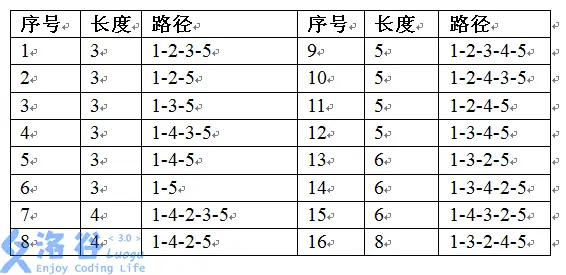
有 $5$ 个城市,所有可能出现的道路均存在。从城市 $1$ 到城市 $5$ 一共有 $5$ 条简单路,排序如下:
Sample 2 Input
4 6 1 1 4
2 4 2
1 3 2
1 2 1
1 4 3
2 3 1
3 4 1
Sample 2 Output
1-2-3-4
Sample 3 Input
3 3 5 1 3
1 2 1
2 3 1
1 3 1
Sample 3 Output
No