There is a grid of $N^2$ squares with $N$ rows and $N$ columns. Let $(i,j)$ denote the square at the $i$-th row from the top $(1\leq i\leq N)$ and $j$-th column from the left $(1\leq j\leq N)$.

Each square is either empty or has a piece placed on it. There are $M$ pieces placed on the grid, and the $k$-th $(1\leq k\leq M)$ piece is placed on square $(a_k,b_k)$.

You want to place your piece on an empty square in such a way that it cannot be captured by any of the existing pieces.

A piece placed on square $(i,j)$ can capture pieces that satisfy any of the following conditions:

• Placed on square $(i+2,j+1)$
• Placed on square $(i+1,j+2)$
• Placed on square $(i-1,j+2)$
• Placed on square $(i-2,j+1)$
• Placed on square $(i-2,j-1)$
• Placed on square $(i-1,j-2)$
• Placed on square $(i+1,j-2)$
• Placed on square $(i+2,j-1)$

Here, conditions involving non-existent squares are considered to never be satisfied.

For example, a piece placed on square $(4,4)$ can capture pieces placed on the squares shown in blue in the following figure:

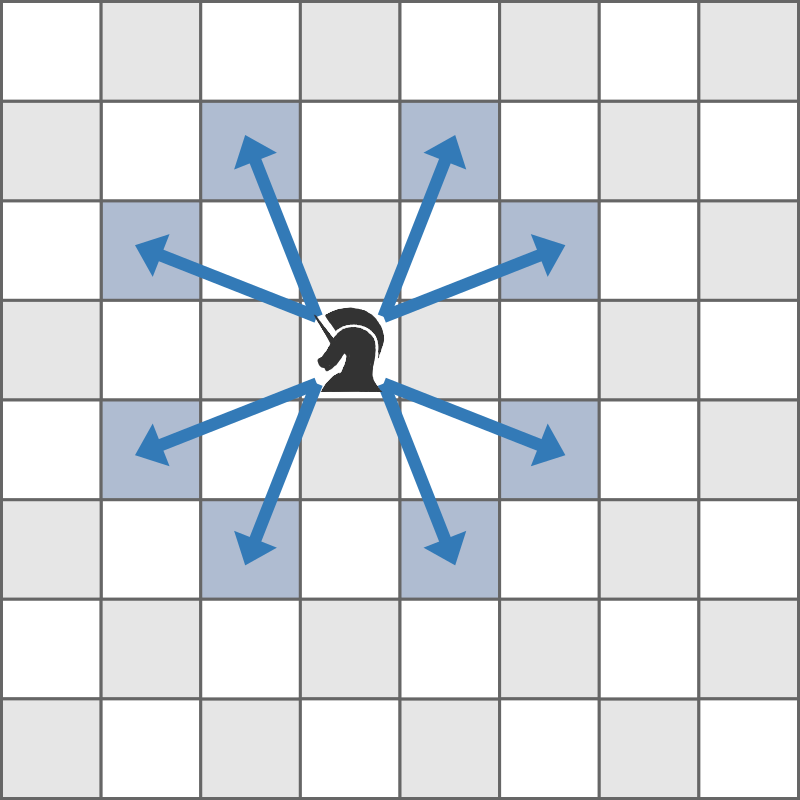
How many squares can you place your piece on?

The input is given from Standard Input in the following format:

$N$ $M$

$a_1$ $b_1$

$a_2$ $b_2$

$\vdots$

$a_M$ $b_M$

Print the number of empty squares where you can place your piece without it being captured by any existing pieces.

• $1\leq N\leq10^9$
• $1\leq M\leq2\times10^5$
• $1\leq a_k\leq N,1\leq b_k\leq N\ (1\leq k\leq M)$
• $(a_k,b_k)\neq(a_l,b_l)\ (1\leq k\lt l\leq M)$
• All input values are integers.

The existing pieces can capture pieces placed on the squares shown in blue in the following figure:

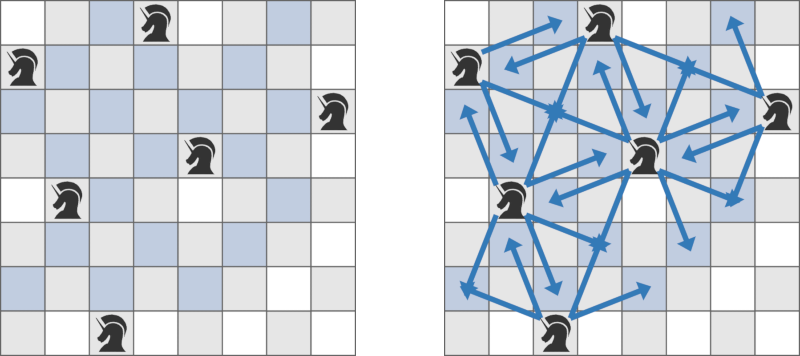
Therefore, you can place your piece on the remaining $38$ squares.

Out of $10^{18}$ squares, only $3$ squares cannot be used: squares $(1,1)$, $(2,3)$, and $(3,2)$.

Note that the answer may be $2^{32}$ or greater.