There is a grid of $64$ squares with $8$ rows and $8$ columns. Let $(i,j)$ denote the square at the $i$-th row from the top $(1\leq i\leq8)$ and $j$-th column from the left $(1\leq j\leq8)$.

Each square is either empty or has a piece placed on it. The state of the squares is represented by a sequence $(S_1,S_2,S_3,\ldots,S_8)$ of $8$ strings of length $8$. Square $(i,j)$ $(1\leq i\leq8,1\leq j\leq8)$ is empty if the $j$-th character of $S_i$ is ., and has a piece if it is #.

You want to place your piece on an empty square in such a way that it cannot be captured by any of the existing pieces.

A piece placed on square $(i,j)$ can capture pieces that satisfy either of the following conditions:

• Placed on a square in row $i$
• Placed on a square in column $j$

For example, a piece placed on square $(4,4)$ can capture pieces placed on the squares shown in blue in the following figure:

How many squares can you place your piece on?

The input is given from Standard Input in the following format:

$S_1$

$S_2$

$S_3$

$S_4$

$S_5$

$S_6$

$S_7$

$S_8$

Print the number of empty squares where you can place your piece without it being captured by any existing pieces.

• Each $S_i$ is a string of length $8$ consisting of . and # $(1\leq i\leq 8)$.

The existing pieces can capture pieces placed on the squares shown in blue in the following figure:

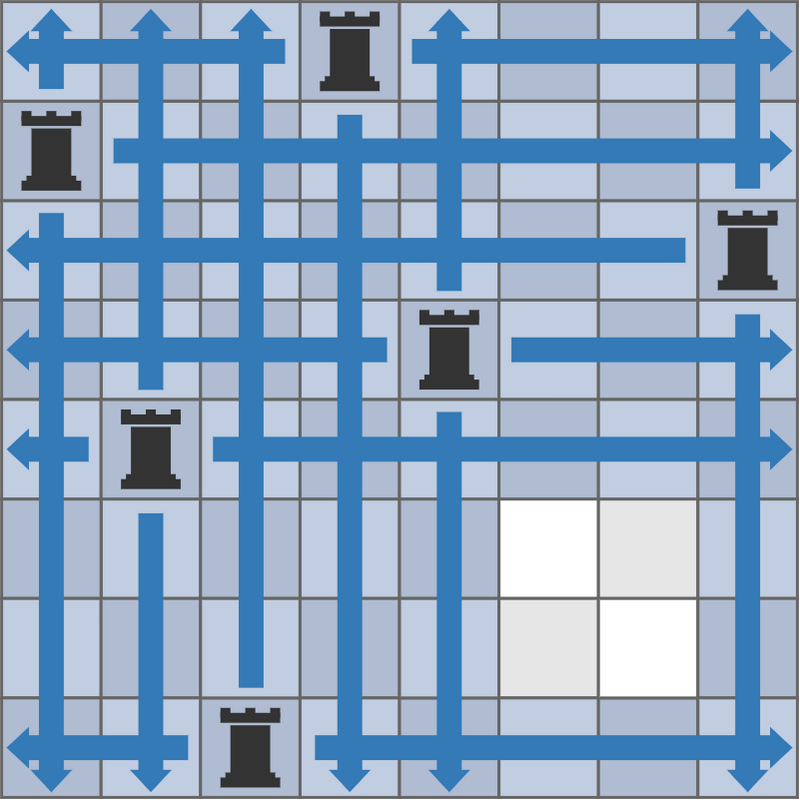
Therefore, you can place your piece without it being captured on $4$ squares: square $(6,6)$, square $(6,7)$, square $(7,6)$, and square $(7,7)$.